Tugas matematika : Juni 2020

Perbandingan Trigonometri :

contoh soal

1. Diketahui segitiga PQR dengan P(0, 1, 4), Q(2, -3, 2), dan R (-1, 0, 2). Besar sudut PQR adalah ….

$\textrm{A.} \; \; \; 120^{o}$

$\textrm{B.} \; \; \; 90^{o}$

$\textrm{C.} \; \; \; 60^{o}$

$\textrm{D.} \; \; \; 45^{o}$

$\textrm{E.} \; \; \; 30^{o}$

Pembahasan:

Segitiga PQR pada soal dapat diilustrasikan seperti berikut.

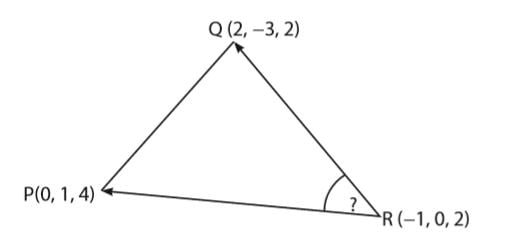
Mencari panjang RQ:

$\overrightarrow{RQ} = (2-(-1), -3-0, 2-2)=(3,-3,0)$

$|RQ|= \sqrt{3^{2}+(-3)^{2}+0^{2}} =\sqrt{9+9+0}= \sqrt{18}$

Mencari panjang RP:

$\overrightarrow{RP} = (0-(-1), 1-0, 4-2)=(1,1,2)$

$|RQ|= \sqrt{1^{2}+1^{2}+2^{2}} =\sqrt{1 + 1 + 4} = \sqrt{6}$

Mencari besar sudut R:

$\overrightarrow{RQ} \cdot \overrightarrow{RP} = |RP| \cdot |RQ| \cdot Cos \; R$

$(3,-3,0)(1,1,2) = \sqrt{18} \cdot \sqrt{6} \cdot Cos \; R$

$3 - 3 + 0 = \sqrt{108} \cdot Cos \; R$

$0 = \sqrt{108} \cdot Cos \; R$

$Cos \; R = \frac{\sqrt{108}}{0}$

$Cos \; R = 0 \rightarrow R = 90^{o}$

Jadi, besar sudut R adalah 90o.

Jawaban: B.

.2 Diketahui siku-siku ABC, siku-siku di C, panjang a = 4 dan b = 3.

Tentukanlah panjang sisi dan nilai perbandingan trigonometri sudut α

Jawab:

3. Diketahui segitiga ABC dengan A(3, 1), B(5, 2), dan C(1, 5). Besar sudut BAC adalah ….

$\textrm{A.} \; \; \; 45^{o}$

$\textrm{B.} \; \; \; 60^{o}$

$\textrm{C.} \; \; \; 90^{o}$

$\textrm{D.} \; \; \; 120^{o}$

$\textrm{E.} \; \; \; 135^{o}$

Pembahasan:

Gambar segitiga ABC yang sesuai pada soal adalah

Mencari panjang AC:

$\overrightarrow{AC} = (1-3, 5-1)=(-2,4)$

$|RQ|= \sqrt{(-2)^{2} + 4^{2}} =\sqrt{ 4 + 4 }= \sqrt{8}$

Mencari panjang AB:

$\overrightarrow{AB} = (5 - 3, 2 - 1) = (2, 1)$

$|RQ|= \sqrt{2^{2} + 1^{2}} =\sqrt{4 + 1} = \sqrt{5}$

Mencari besar sudut A:

$\overrightarrow{AC} \cdot \overrightarrow{AB} = |AC| \cdot |AB| \cdot Cos \; A$

$(-2,4) \cdot (2, 1) = \sqrt{8} \cdot \sqrt{5} \cdot Cos \; A$

$-4 + 4 = \sqrt{40} \cdot Cos \; A$

$0 = \sqrt{40} \cdot Cos \; A$

$Cos \; A = \frac{\sqrt{40}}{0}$

$Cos \; A = 0 \rightarrow A = 90^{o}$

Jadi, besar sudut A adalah 90o.

Jawaban: C

4. Jika cos(γ) =

\frac{\sqrt{2}}{2}

dan sudut γ lancip, tentukan nilai dari

c s c^{2} (γ) - c o t^{2} (γ)

Pembahasan :
cos(γ) =

\frac{s a m p i n g}{m i r i n g}

\frac{\sqrt{2}}{2}

samping =

\sqrt{2}

miring = 2
depan =

\sqrt{2^{2} - (\sqrt{2})^{2}}

\sqrt{2}

Sesuai definisi
csc(γ) =

\frac{2}{\sqrt{2}}

cot(γ) =

\frac{\sqrt{2}}{\sqrt{2}}

= 1

csc²(γ) − cot²(γ) = (

\frac{2}{\sqrt{2}}

)² − (1)²
csc²(γ) − cot²(α) = 2 − 1
csc²(γ) − cot²(α) = 1

Jadi, csc²(γ) − cot²(γ) = 1

5. Jika sin(β) =

\frac{1}{2}

dan sudut β lancip, tentukan nilai dari

s e c^{2} (β) - t a n^{2} (β)

Pembahasan :
sin(β) =

\frac{d e p a n}{m i r i n g}

\frac{1}{2}

depan = 1
miring = 2
samping =

\sqrt{2^{2} - 1^{2}}

\sqrt{3}

Sesuai definisi
sec(β) = $\frac{2}{\sqrt{3}}$
tan(β) = $\frac{1}{\sqrt{3}}$

sec²(β) − tan²(β) = ( $\frac{2}{\sqrt{3}}$ )² − ( $\frac{1}{\sqrt{3}}$ )²
sec²(α) − tan²(α) = $\frac{4}{3}$ − $\frac{1}{3}$
sec²(α) − tan²(α) = 1

Jadi, sec²(β) − tan²(β) = 1

Sudut Berelasi

contoh soal

1. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya

sin 20°
tan 40°
cos 53°

Jawab :
sin 20° = sin (90° − 70°)
= cos 70°

tan 40° = tan (90° − 50°)
= cot 50°

cos 53° = cos (90° − 37°)
= sin 37°

2. Tentukan nilai dari

\frac{s i n 100^{\circ} - c o s 190^{\circ}}{c o s 350^{\circ} - s i n 260^{\circ}}

Pembahasan :

sin 100° = sin (90° + 10°) = cos 10°
cos 190° = cos (180° + 10°) = -cos 10°
cos 350° = cos (360° − 10°) = cos 10°
sin 260° = sin (270° − 10°) = -cos 10°
Sehingga :

\frac{s i n 100^{\circ} - c o s 190^{\circ}}{c o s 350^{\circ} - s i n 260^{\circ}} = \frac{c o s 10^{\circ} - (- c o s 10^{\circ})}{c o s 10^{\circ} - (- c o s 10^{\circ})} = \frac{2 c o s 10^{\circ}}{2 c o s 10^{\circ}} = 1

3. Diketahui cot (x + 36°) = tan 2x. Jika 2x adalah sudut lancip, tentukan nilai x !

Pembahasan :
cot (x + 36°) = tan 2x
Karena 2x sudut lancip, pastilah 2x terletak dikuadran I. Dengan menggunakan relasi sudut kuadran I, maka :
tan 2x = cot (90° − 2x)

Sehingga
cot (x + 36°) = cot (90° − 2x)
x + 36 = 90° − 2x
3x = 54
x = 18

4. Jika (x + 20°) adalah sudut lancip, tentukan nilai dari

\frac{t a n (x + 110^{\circ})}{2 c o t (x + 20^{\circ})}

Pembahasan :
tan (x + 110°) = tan (90° + (x + 20°))
Karena (x + 20°) lancip, maka (90° + (x + 20°)) adalah sudut kuadran II, sehingga tangen bernilai negatif.
tan (90° + (x + 20°)) = -cot (x + 20°)

akibatnya

\frac{t a n (x + 110^{\circ})}{2 c o t (x + 20^{\circ})} = \frac{- c o t (x + 20^{\circ})}{2 c o t (x + 20^{\circ})} = - \frac{1}{2}

Aturan Sinus Cosinus dan luas segitiga

contoh soal

Sinus

1. Diketahui suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit sebesar 60o dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan 16 meter, maka luas taman tersebut adalah ….

$\textrm{A.} \; \; \; 72 \; \textrm{m}^{2}$

$\textrm{B.} \; \; \; 72 \sqrt{2} \; \textrm{m}^{2}$

$\textrm{C.} \; \; \; 72 \sqrt{3} \; \textrm{m}^{2}$

$\textrm{D.} \; \; \; 144 \textrm{m}^{2}$

$\textrm{E.} \; \; \; \frac{\sqrt{106}}{4} \; \textrm{m}^{2}$

Pembahasan:

Untuk menentukan luas segitiga sembarang yang diketahui panjang dua sisi dan sudut antara kedua sisi tersebut dapat memanfaatkan fungsi sinus.

$L = \frac{1}{2} \times 18 \times 16 \times sin \; 60^{o}$

$L = \frac{1}{2} \times 18 \times 16 \times \frac{1}{2} \sqrt{3}$

$L = 72 \sqrt{3} \; \textrm{m}^{2}$

Jawaban: C.

2. Di sebuah museum terdapat miniatur piramida berbentuk limas segiempat beraturan. Dari data museum diketahui panjang rusuk tegak piramida 4 meter dan membentuk sudut 30o di puncaknya. Luas satu sisi tegak piramida tersebut adalah ….

A. 40 dm2

B. 80 dm2

C. 400 dm2

D. 800 dm2

E. 4.000 dm2

Pembahasan:

Perhatikan gambar di bawah!

Jadi, luas satu sisi tegak piramida tersebut adalah

$L = \frac{1}{2} \times 4 \times 4 \times Sin \; 30^{o}$

$L = \frac{1}{2} \times 4 \times 4 \times \frac{1}{2}$

$L = 4 \; \textrm{m}^{2} = 400 \; \textrm{dm}^{2}$

Jawaban: C

cosinus

1. Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 60 mil dengan arah $40^{o}$ dari A, kemudian berputar haluan dilanjutkan ke pelabuhan C sejauh 90 mil dengan arah $160^{o}$ dari B. Jarak terdekat dari pelabuhan A ke C adalah ….

$\textrm{A.} \; \; \; 30 \sqrt{2}$

$\textrm{B.} \; \; \; 30 \sqrt{5}$

$\textrm{C.} \; \; \; 30 \sqrt{7}$

$\textrm{D.} \; \; \; 30 \sqrt{10}$

$\textrm{E.} \; \; \; 30 \sqrt{30}$

Pembahasan:

Perhatikan gambar di bawah!

Jarak terdekat dari pelabuhan A ke C dapat dicari dengan aturan cosinus:

Jadi, jarak terdekat dari pelabuhan A ke C adalah $30 \sqrt{7}$ mil.

Jawaban: C

2. Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B sejauh 40 mil dengan arah $30^{o}$ dari A kemudian berputar haluan dilanjutkan ke pelabuhan C sejauh 60 mil dengan arah $150^{o}$ dari B. Jarak terdekat dari pelabuhan A dan C adalah ….

$\textrm{A.} \; \; \; 20 \sqrt{2} \; \textrm{mil}$

$\textrm{B.} \; \; \; 20 \sqrt{3} \; \textrm{mil}$

$\textrm{C.} \; \; \; 20 \sqrt{5} \; \textrm{mil}$

$\textrm{D.} \; \; \; 20 \sqrt{7} \; \textrm{mil}$

$\textrm{E.} \; \; \; 20 \sqrt{11} \; \textrm{mil}$

Pembahasan:

Perhatikan gambar di bawah!

Jarak terdekat dari pelabuhan A ke C dapat dicari dengan aturan cosinus:

Jadi, jarak terdekat dari pelabuhan A ke C adalah $20 \sqrt{7}$ mil.

Jawaban: D.

Persamaan Trigonometri

contoh soal

1. Tentukan penyelesaian persamaan soal pers sin.png

dalam interval 0 ≤ x ≤ 2π

Jawab:

2. Untuk 0° ≤ x ≤ 360° tentukan himpunan penyelesaian dari cos x = ½ ….

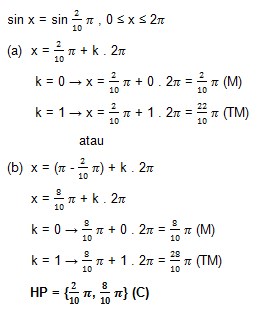
Penyelesaian :

3. Tentukan nilai x yang memenuhi persamaan 2 sin x = 1 , dengan 0o ≤ x ≤ 360o ….

Penyelesaian :

4. Tentukan himpunan penyelesaian dari persamaan trigonometri sin x = sin 2/10 π, 0 ≤ x ≤ 2π …..

Penyelesaian :

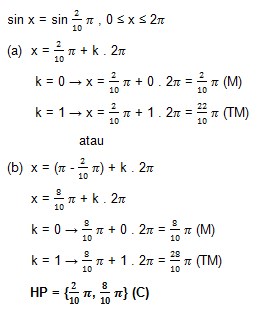
Grafik Trigonometri

contoh soal

Persamaan grafik fungsi pada gambar di atas adalah ….

A. y = – 2 Sin(3x + 45)o

B. y = – 2 Sin(3x – 45 )o

C. y = – 2 Sin(3x – 45 )o

D. y = 2 Sin(3x + 15)o

E. y = 2 Sin(3x – 45 )o

Pembahasan:

Berdasarkan grafik fungsi trigonometri pada soal dapat diperoleh informasi:

Nilai Amplitudo: A = 2
Periode dari 15o sampai 135o adalah 1, sehingga:
   $\frac{360^{o}}{k} = 135^{o} - 15^{o}$

   $\frac{360^{o}}{k} = 120^{o}$

   $k = \frac{360^{o}}{120^{o}} = 3$
Grafik fungi trigonometri pada soal merupakan grafik dasar fungsi sinus y = Sin x yang digeser ke kana sejauh 15o.

Persamaan umum fungsi sinus adalah:

$y = A \cdot Sin \; k \left(x \pm \alpha \right)^{o} \pm C$

Jadi, persamaan grafik fungsi trigonometri yang sesuai dengan gambar pada soal adalah:

$y = 2 \cdot Sin \; 3 \left(x - 15 \right)^{o}$

$y = 2 \cdot Sin \; \left(3x - 45 \right)^{o}$

Jawaban: E

Persamaan fungsi trigonometri yang sesuai pada grafik di atas adalah ….

Penyelesaian :

Grafik fungsi trigonometri merupakan bentuk grafik fungsi sinus. Persamaan umum grafik fungsi trigonometri untuk fungsi sinus adalah:

$y = A \; \textrm{Sin} \; k (x \pm \alpha ) \pm c$

Menghitung banyaknya gelombang dalam 1 periode (k):

Berdasarkan informasi grafik fungsi trigonometri yang diberikan pada soal, diketahui bahwa pada rentang $- \frac{pi}{6}$ sampai dengan $\frac{5 \pi }{6}$ memuat setengah periode.

$\frac{\pi}{k} = \left( \frac{5 \pi}{6} - \left( - \frac{\pi}{6} \right) \right)$

$\frac{ \pi }{k} = \frac{5 \pi}{6} + \frac{\pi}{6}$

$\frac{ \pi }{k} = \frac{6 \pi}{6}$

$k = \frac{6 \pi}{6 \pi} = 1$

Jadi banyaknya gelombang dalam satu periode adalah 1 (k = 1).

Mencari nilai Amplitudo (A): nilai tertinggi yang dapat dicapai grafik fungsi trigonometri adalah 2 atau – 2 , sehingga nilai amplitudonya sama dengan 2 (A = 2).

Grafik fungsi trigonometri yang diberikan pada soal bergeser sejauh 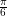$\frac{\pi}{6}$ ke arah kiri, sehingga persamaan akan mendapat tambahan + ${\pi}{6}$ .

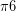Jadi, persamaan grafik fungsi trigonometri yang sesuai dengan soal adalah:

$y = 2 \cdot Sin \; 1 \left( x + \frac{\pi}{6} \right)$

= $y = 2 Sin \left( x + \frac{\pi}{6} \right)$

3. Grafik f(x)= 2 cos x memotong sumbu-X di titik berkoordinat...

Pembahasan:

Apabila grafik memotong sumbu-

X

, maka nilai

f (x) = y = 0

. Dengan demikian,

f (x) = 2 \cos x \Rightarrow 0 = 2 \cos x \Leftrightarrow \cos x = 0

Nilai

x

yang membuat

\cos x

bernilai 0 adalah

90^{\circ}

.
Jadi, titik potong grafiknya berkoordinat

(90^{\circ}, 0)

Tugas matematika

Senin, 15 Juni 2020

Soal Trigonometri

pembelajaran online

Laporkan Penyalahgunaan