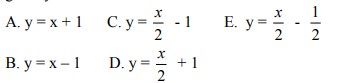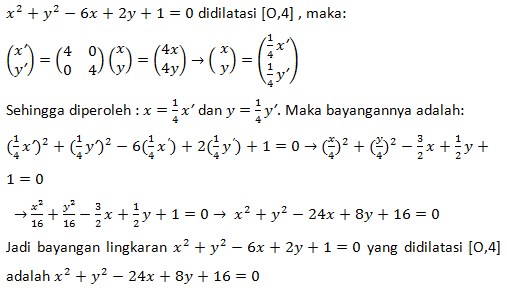nama : tabitha fransisca r.n
kelas : xi ips 3
absen 35
contoh soal
TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI
1. Tentukan bayangan titik (3,-7) oleh translasi
(42)
Pembahasan:
Misalkan titik P(3,-7).
T = ( (42)) : P(3,-7) → P'(3+4 , -7+2) = P'(7,-5)
Jadi, bayangan titik (3,-7) oleh translasi (42) adalah (7,-5)
2. Titik P'(2,-4) adalah bayangan titik P(3,5) oleh translasi T. Tentukanlah translasi T.
Pembahasan:
T = (ab) : P(3,5) → P'(3+a , 5+b) = P'(2,-4)
Sehingga diperoleh:
3 + a = 2 => a = -1
5 + b = -4 => b = -9
Jadi, translasi T = (−1−9).
3. Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .
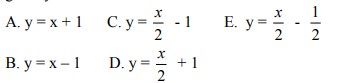
Jawaban : C
Pembahasan :

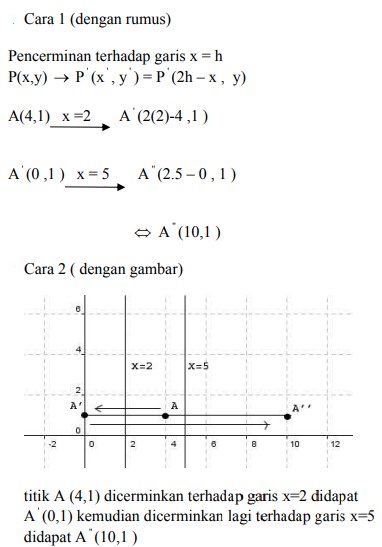
4. Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik….
A. A” (8,5)
B. A” (10,1)
C. A” (8,1)
D. A” (4,5)
E. A” (20,2)
Jawaban : B
Pembahasan :
5.
Tentukan persamaan peta dari garis 3x – 5y + 15 = 0 oleh pencerminan terhadap sumbu x!
Jawaban :
Pembahasan :

6. Jika garis x - 2y = 5 diputar sejauh 90⁰ terhadap titik (2,4) berlawanan arah putaran jam, maka tentukanlah persamaan bayangannya.
Pembahasan:
(x′y′)=(01−10).(x−2y−4)+(24)
⟺ (x′y′)=(4−yx−2)+(24)
⟺ (x′y′)=(6−yx+2)
Dengan demikian, maka:
x' = 6 - y => y = 6 - x'
y' = x + 2 => x = y' - 2
Dengan mensubtitusikan x = y' - 2 dan y = 6 - x' pada persamaan garis, diperoleh:
(y' - 2) - 2(6 - x') = 5
y' - 2 - 12 + 2x' = 5
2x' + y' = 5 + 2 + 12
2x' + y' = 19
Jadi, persamaan bayangan garis x - 2y = 5 oleh rotasi sejauh 90⁰ terhadap titik (2,4) berlawanan arah putaran jam adalah 2x + y = 19.
7. Titik B(5,-1) dirotasikan terhadap titik P(2,3) sejauh 90⁰ searah putaran jam. Tentukanlah bayangan titik B tersebut.
Pembahasan:
(x′y′)=(0−110).(x−ay−b)+(ab)
⟺ (x′y′)=(0−110).(5−2−1−3)+(23)
⟺ (x′y′)=(0−110).(3−4)+(23)
⟺ (x′y′)=(−4−3)+(23)
⟺ (x′y′)=(−20)
Dengan demikian, x' = -2 dan y' = 0.
Jadi, koordinat bayangan titik B(5,-1) oleh rotasi terhadap titik P(2,3) sejauh 90⁰ searah putaran jam adalah B'(-3,0).
8. Tentukan persamaan peta dari garis 3x-5y+15=0 oleh dilatasi terhadap pusat O(0,0) dengan faktor skala 5!
Jawaban :
Pembahasan :

9. Lingkaran x² + y² – 6x + 2y + 1 = 0. Jika ditransformasikan dengan dilatasi [O,4], persamaan bayangannya adalah….
Jawaban :
Pembahasan :
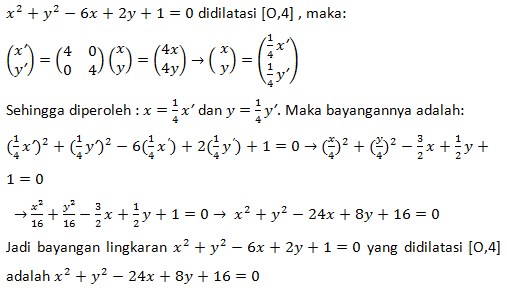
10. Tentukanlah bayangan titik P(2,-1) oleh dilatasi terhadap titik pusat A(3,4) dengan faktor skala -3.
Pembahasan:
(x′y′)=(k00k).(x−ay−b)+(ab)
⟺ (x′y′)=(−300−3).(2−3−1−4)+(34)
⟺ (x′y′)=(−300−3).(−1−5)+(34)
⟺ (x′y′)=(315)+(34)
⟺ (x′y′)=(619)
Dengan demikian x' = 6 dan y' = 19.
Jadi, bayangan titik P(2,-1) oleh dilatasi terhadap titik pusat A(3,4) adalah P'(6,19).
DAFTAR PUSTAKA
http://ilmuku-duniaku14.blogspot.com/2018/06/kumpulan-soal-dan-pembahasan-translasi.html http://ilmuku-duniaku14.blogspot.com/2018/07/soal-dan-pembahasan-rotasi-perputaran.html
http://ilmuku-duniaku14.blogspot.com/2018/07/soal-dan-pembahasan-dilatasi-perkalian.html
https://soalkimia.com/contoh-soal-transformasi-geometri/