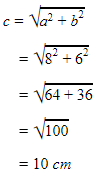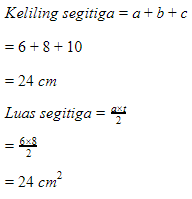Nama : Tabitha Fransisca R.N
Kelas : X ips 3
Absen: 35
Sekolah : SMAN 63 Jakarta Selatan
Materi pelajaran matematika yang disukai.
Materi yang saya sukai di semester 2 ini adalah aturan sinus dan cosinus. Karna pada materi ini berpatok pada sudut sudut. Juga dengan rumus yang tetap. Walaupun materi ini tidak banyak dibahas di kelas, tapi saya suka materi ini karna rumusnya ga ribet. Kalau kita tau rumus pasti bisa mengerjakan dengan baik dan benar.
Senin, 04 Mei 2020
contoh soal dan pembahasan
3.7 Menyelesaikan cara merubah satuan pengukuran sudut trigonometri radian ke derajat, derajat ke radian
1. Nyatakan sudut 50° dan 89° ke dalam radian!
Jawab:
50° = 50° x π/180°
50° = 0,277π
50° = 0,277 (3,14)
50° = 0,87 radian
50° = 50° x π/180°
50° = 0,277π
50° = 0,277 (3,14)
50° = 0,87 radian
89° = 89° x π/180°
89° = 0,494π
89° = 0,494 (3,14)
89° = 1,55 radian
89° = 0,494π
89° = 0,494 (3,14)
89° = 1,55 radian
2. Nyatakan sudut 0,45 radian dan 0,89 radian ke dalam satuan derajat!
Jawab:
0,45 radian = 0,45 x 180°/π
0,45 radian = 25,80°
0,45 radian = 0,45 x 180°/π
0,45 radian = 25,80°
0,89 radian = 0,89 x 180°/π
0,89 radian = 51,02°
0,89 radian = 51,02°
3. 15° berapa radian?
Jawab:15° = 15 x (π/180) = 0,265 radian
4. Hitunglah sudut 2,2 radian dalam derajat!
2,2 radian = 2,2 x (180°/π) = 126°
3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku dan dudut istimewa (600 , 300 , 450 )
, nilai yang memenuhi adalah...

a. 3√5
b. 4√5
c. 5√5
d. 6√5
e. 7√5
Jawab:
Tanpa memperhatikan gambar segitiga siku-siku yang diberikan, panjang sisi depan sudut dapat dihitung dengan menggunakan Teorema Pythagoras.
Dalam hal ini, karena , maka dimisalkan dan , sehingga
Dengan demikian,
Berdasarkan gambar yang diberikan, haruslah . Akibatnya,
Jadi, nilai adalah
Jawaban a
Dalam hal ini, karena , maka dimisalkan dan , sehingga
Dengan demikian,
Berdasarkan gambar yang diberikan, haruslah . Akibatnya,
Jadi, nilai adalah
Jawaban a
3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku di dalam koordinat kartesius
1. besar sudut yang sesuai dengan gambar dibawah ini adalah...

a. 30º d. 330º
b. 60 º e. 390º
c. 300º
Jawab:
sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni
.Karena satu putaran sama dengan , maka sama dengan
Jadi, besar sudutnya adalah 330º
2. Besar sudut sama dengan
A. C. E.
B. D.
A. C. E.
B. D.
Jawab:
Ingat bahwa
Dengan demikian,
Jadi, besar sudut sama dengan
Jawaban b
= cos 70°
tan 40° = tan (90° − 50°)
= cot 50°
tan 143° = tan (180° − 37°)
= -tan 37°
Sudut 233° ada pada kuadran III, sehingga sinus mempunyai nilai negatif.
sin 233° = sin (270° − 37°)
= -cos 37°
nilai dari sin 30° . cos 60° + sin 60° . cos 30°
Dengan demikian,
Jadi, besar sudut sama dengan
Jawaban b
3.7 Menyelesaikan nilai trigonometri pada suatu sudut segitiga siku-siku pada koordinat cartesius
Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
v sin 20°
pembahasan :
sin 20° = sin (90° − 70°)= cos 70°
v tan 40°
pembahasan :tan 40° = tan (90° − 50°)
= cot 50°
o Nyatakan tiap perbandingan trigonometri berikut di dalam sudut 37° !
v tan 143°
pembahasan :
Sudut 143° adapada kuadran II, sampai tan 143° mempunyai nilai negatif.pembahasan :
tan 143° = tan (180° − 37°)
= -tan 37°
v sin 233°
pembahasan :Sudut 233° ada pada kuadran III, sehingga sinus mempunyai nilai negatif.
sin 233° = sin (270° − 37°)
3.7 Menyelesaikan komposisi operasi (+, -, :, dan •) nilai trigonometri
Pembahasan :
sin 30° . cos 60° + sin 60° . cos 30°
1/2 . 1/2 + 1/2 . 1/2
1/4 + 1/4 .
1/4 + 1/4 . 3
1/4 + 3/4
4/4
= 1
3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut di berbagai kuadran
1. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya



B.
C.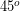
D.
E.
Jadi, tinggi menara adalah
Jawaban a
2. Sisno diminta mengukur tinggi tiang bendera menggunakan klinometer. Saat pertama berdiri dengan melihat ujung tiang bendera, terlihat pada klinometer menunjuk pada sudut 60o. Kemudian ia bergerak menjauhi tiang bendera sejauh 10 meter dan terlihat pada klinometer sudut 45o. Tinggi tiang bendera adalah ….
Jawab:

Mencari nilai t:
Mencari nilai x:
Kalikan dengan akar sekawan:
Jadi, tinggi tiang bendera (t) adalah
Jawaban b
3.9 Menyelesaikan aturan sinus diketahui 2 sudut dan 1 sisi
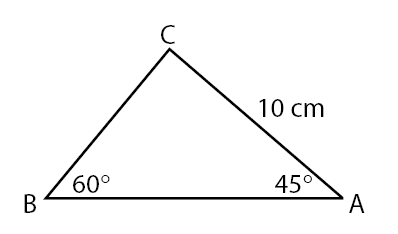
1. Suatu segitiga ABC memiliki panjang AC = 8 cm. Jika besar  dan
dan  , maka panjang BC = … cm.
, maka panjang BC = … cm.
Panjang BC dapat dicari menggunakan aturan sinus.
Jawaban e
3.9 Menyelesaikan aturan sinus diketahui 1 sudut dan 2 sisi
1. Diketahui suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit sebesar 60o dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan 16 meter, maka luas taman tersebut adalah ….
Jawab:
Untuk menentukan luas segitiga sembarang yang diketahui panjang dua sisi dan sudut antara kedua sisi tersebut dapat memanfaatkan fungsi sinus.
Jawaban c
2. Di sebuah museum terdapat miniatur piramida berbentuk limas segiempat beraturan. Dari data museum diketahui panjang rusuk tegak piramida 4 meter dan membentuk sudut 30o di puncaknya. Luas satu sisi tegak piramida tersebut adalah ….
A. 40 dm2
B. 80 dm2
C. 400 dm2
D. 800 dm2
E. 4.000 dm2
Jawab:

Jadi, luas satu sisi tegak piramida tersebut adalah
Jawaban c
3.9 Menyelesaikan aturan cos ditanya sisi
1. Segitiga ABC diketahui panjang sisi a = 5 cm, panjang sisi c = 6 cm dan besar sudut B = 60º. Tentukan panjang sisi b
dik: a = 5 cm
c = 6 cm
B = 60º
dit: b?
Jawab:
b2 = a2 + c2 - 2ac cos B
b2 = 52 + 62 - 2(5)(6) cos 60º
b2 = 25 + 36 - 60 (0,5)
b2 = 61 - 30
b2 = 31
b = 5,56 cm
Jadi, panjang sisi b adalah 5,56 cm
3.9 Menyelesaikan aturan cos ditanya sudut
1. Pada suatu segitiga dengan sisi-sisi a, b, dan c memenuhi  . Maka besar sudut A adalah ….
. Maka besar sudut A adalah ….
A. B.
C.
D.
E.
Jawab:
Diketahui:
Sehingga,
Salah satu rumus cosinus adalah:
Berdasarkan dua persamaan di atas, akan diperoleh nilai cos A.
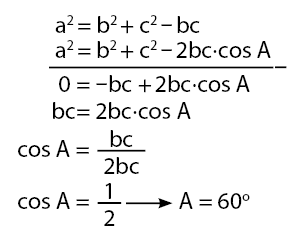
2. Sebuah segitiga ABC memiliki sisi-sisi a, b dan c. Pada segitiga tersebut berlaku (a − b)(a + b) = c (c − b √3 ) . Tentukan besar sudut A
Jawab:
Diketahui:
(a −b)(a + b) = c (c − b √3 )
Uraikan
a2 − b2 = c2 − bc√3
a2 = b2 + c2 − bc√3
Dari aturan kosinus
a2 = b2 + c2 − 2bc cos A
Terlihat bahwa 2bc cos A = bc√3 sehingga
2bc cos A = bc√3
cos A = 1/2 √3
A = 30º
Sudut dengan nilai cos sebesar 1/2 √3 adalah 30º.
Uraikan
a2 − b2 = c2 − bc√3
a2 = b2 + c2 − bc√3
Dari aturan kosinus
a2 = b2 + c2 − 2bc cos A
Terlihat bahwa 2bc cos A = bc√3 sehingga
2bc cos A = bc√3
cos A = 1/2 √3
A = 30º
Sudut dengan nilai cos sebesar 1/2 √3 adalah 30º.
3.9 Menyelesaikan Luas segitiga jika diketahui: 1 sudut 2 sisi, 3 sisi, 2 sudut 1 sisi
1. Diketahui sebuah segitiga siku-siku dengan panjang alasnya 8 cm dan tinggi 6 cm. Hitunglah keliling dan luas segitiga tersebut!
Jawab:
Karena segitiga tersebut merupakan segitiga sama sisi, sehingga ketiga sisinya sama panjang.
a = 6 cm
t = 8 cm
Untuk menghitung keliling segitiga tersebut, kita mencari sisi miringnya terlebih dahulu dengan dalil phytagoras. Misalkan sisi miring kita simbolkan dengan c, sehingga
c² = a² + b²
3.10 Menyelesaikan gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
1. Grafik di atas adalah grafik fungsi

Grafik di atas merupakan modifikasi grafik cosinus (karena tidak dimulai dari garis normal di sumbu-) dengan bentuk umum .
Grafik juga menunjukkan bahwa nilai maksimum fungsinya , sedangkan nilai minimumnya , sehingga
Grafik juga menunjukkan bahwa nilai maksimum fungsinya , sedangkan nilai minimumnya , sehingga
PEMBAHASAN :
Saat , nilai fungsinya , lalu berulang kembali di , sehingga periodenya . Dengan demikian, .
Jadi, grafik fungsi di atas adalah grafik fungsi
3.10 Menyelesaikan membaca gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
1. Diketahui f(x) = sin(cos x)
PEMBAHASAN :
f"(x) = - (cos x) . (cos (cos x)) – (sin x) . (sin x) . (sin (cos x))
2. Temukan turunan pertama dari f (x) = tan x + Sec x
PEMBAHASAN :
f''(x) = sec 2x + Sec x tan x = Sec x ( Sec x + tan x)
3.7 Menyelesaikan sudut , sudut depresi
1. 

Diketahui seseorang yang berada di atas mercusuar dengan tinggi meter sedang mengamati sebuah objek di bawahnya dengan jarak antara objek dan mercusuar sejauh meter. sudut depresi yang terbentuk adalah...
a. 30º d. 90º
b. 45º e. 180º
c.60º
Jawab:

Besar sama dengan sudut karena saling berseberangan. Dengan menggunakan konsep tangen, diperoleh
Jadi, sudut depresi yang terbentuk adalah 30º
Jawaban a
Jadi, sudut depresi yang terbentuk adalah 30º
Jawaban a