Tabitha Fransisca R.N
XI IPS 3
No. absen 35
REMEDIAL PAS
5. Pembahasan :
(Benar)
2) asumsikan benar untuk
(
3) cek kebenaran untuk
akan terbukti benar jika
bisa buktikan itu dengan induksi lagi
buktikan bahwa
1) cek kebenaran untuk
(benar)
2) asumsikan benar untuk
3) cek kebenaran untuk
terbukti bahwa
maka pernyataan awal tadi juga benar
- n_ >5 = {1,2,3,4,5}
x | 0 | 3 |
y | 5 | 0 |
(x,y) | (0,5) | (3,0) |
x | 0 | 3 |
y | 5 | 0 |
(x,y) | (0,5) | (3,0) |


LANGKAH PERTAMA (I)
Buatlah sistem pertidaksamaan pada setiap garis dengan menggunakan cara sebagai berikut :
Persamaan garis I melalui titik (0,6) dan (10,0) sehingga :
ax + by = ab
6x + 10y = 6.10
6x + 10y = 60 .... (÷2)
3x + 5y = 30
Kemudian perhatikan daerah arsiran yang mengarah ke bawah atau melalui titik (0,0). Jika arsiran melalui titik (0,0) maka jika diuji titik (0,0) pernyataan dikatakan benar :
3x + 5y = 30
3.0 + 5.0 = 30
0 + 0 = 30
0 ≤ 30 (Benar)
Pertidaksamaannya : 3x + 5y ≤ 30
Persamaan garis II melalui titik (0,-4) dan (2,0) sehingga :
ax + by = ab
-4x + 2y = (-4).2
-4x + 2y = -8 .... (÷ 2)
-2x + y = -4
Kemudian perhatikan daerah arsiran yang mengarah ke sisi kiri atau melalui titik (0,0). Jika arsiran melalui titik (0,0) maka jika diuji titik (0,0) pernyataan dikatakan benar :
-2x + y = -4
(-2).0 + 0 = -4
0 + 0 = -4
0 ≥ -4 (Benar)
Pertidaksamaannya :
-2x + y ≥ -4 .... (× -1)
2x - y ≤ 4
Kemudian pada arsiran juga terdapat garis x ≥ 0 dan y ≥ 0.
Sehingga pertidaksamaannya adalah :
3x + 5y ≤ 30 ; 2x - y ≤ 4 ; x ≥ 0 dan y ≥ 0.
MODEL | POLOS | GARIS | HARGA |
x | 1 | 3 | Rp 150.000 |
y | 2 | 1 | Rp 100.000 |
Stok | 20 | 20 | Maksimum |
Diket :
Ditanya:
det C...?
Jawab :
- mencari matriks C
- mencari det C
det C = (3)(3) - (-6)(8)
= 9 + 48
det C = 57
Jadi, determinan dari matriks C adalah 57.
Diketahui :
A =
Matriks A tidak mempunyai invers
Ditanyakan :
x = .... ?
Jawab :
Jadi,
|A| = 0
(2x + 1)(5) – 3(6x – 1) = 0
10x + 5 – 18x + 3 = 0
8 – 8x = 0
8 = 8x
x =
x = 1

- Agar lebih mudah dalam membuat matriks produksi, pertama kita akan membuat tabel produksi untuk masing-masing pabrik sebagai berikut.
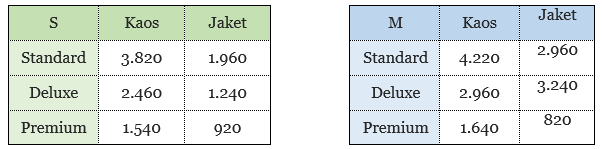
Sehingga, kita mendapatkan matriks-matriks produksi S dan M sebagai berikut.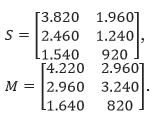
- Dari matriks yang diperoleh dari poin 1, kita dapat menghitung banyaknya pakaian yang telah diproduksi oleh pabrik di Surabaya. Banyaknya kaos yang telah diproduksi adalah 7.820, sedangkan banyaknya jaket yang sudah diproduksi adalah 4.120. Selanjutnya, banyaknya kaos yang diproduksi oleh pabrik di Malang adalah 8.820, sedangkan banyaknya jaket yang telah diproduksi adalah 7.020.
- Diketahui perkiraan peningkatan produksinya adalah 4% = 0,04. Artinya, jika n adalah banyaknya produksi pakaian tahun kemarin, maka banyaknya produksi pada tahun ini adalah n + 0,04n = 1,04n. Sehingga, matriks produksi pada tahun depan dapat ditentukan dengan menggunakan perkalian skalar sebagai berikut.
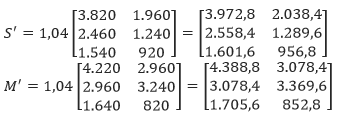
Sehingga dari matriks di atas kita mendapatkan perkiraan banyaknya pakaian yang akan diproduksi oleh JCloth di pabrik Surabaya ataupun Malang. Pabrik di Surabaya akan memproduksi kaos kurang lebih 3.973 kualitas standard, 2.558 kualitas deluxe, dan 1.602 kualitas premium serta memproduksi jaket sebanyak 2.038 kualitas standard, 1.290 kualitas deluxe, dan 956,8 kualitas premium. Sedangkan pada, pabrik di Malang akan memproduksi kaos sebanyak 4.389 kualitas standard, 3.078 kualitas deluxe, 1.706 kualitas premium serta meproduksi jaket sebanyak 3.078 kualitas standard, 3.370 kualitas deluxe, dan 852,8 kualitas premium pada periode yang sama. - Untuk menentukan banyaknya total pakaian yang diproduksi oleh JCloth, kita jumlahkan matriks S’ dengan M’ seperti berikut.

Dari penjumlahan matriks di atas, kita memperoleh informasi banyaknya pakaian yang akan diproduksi oleh JCloth. Dengan menjumlahkan semua elemen-elemen matriks penjumlahan tersebut, kita peroleh bahwa banyaknya pakaian yang akan diproduksi oleh JCloth kurang lebih 28.142.
x + y = 16
3x + 4y = 55
Jika ditulis dalam bentuk matriks :
Jadi, Lisa bekerja selama 9 jam sedangkan Muri bekerja selama 7 jam.
26. Pembahasan :
Bayangan titik A (-1, 4) oleh refleksi terhadap garis y= -x
Pencerminan terhadap garis y = -x
A(a, b) → gr y = -x → A'(-b, -a)
A(-1, 4) → gr y = -x → A'(-4, -(-1)) = (-4, 1)
27. Pembahasan :
(x, y) dicerminkan thp sumbu x : (x, -y) kemudian
(x, -y) dicerminkan thp sumbu y : (-x, -y)
Jadi
-x = x' => x = -x'
-y = y' => y = -y'
Bayangan dari : y = 3x² + 2x - 1 adalah
(-y') = 3(-x')² + 2(-x') - 1
-y' = 3x'² - 2x' - 1
y = -3x² + 2x + 1
28. Pembahasan :
Bayangan titik (x, y) oleh transformasi T :
Dari persamaan matriks diatas, diperoleh :
x' = -x ↔ x = -x'
y' = y ↔ y = y'
Substitusi x dan y ke persamaan kurva :
3x + 5y − 2 = 0
⇒ 3(-x') + 5(y') − 2 = 0
⇔ -3x' + 5y' − 2 = 0
⇔ 3x' − 5y' + 2 = 0
Jadi, persamaan bayangan kurva adalah :
3x − 5y + 2 = 0
Step-1 pencerminan garis x = k
Untuk x = 2
(x' , y') = (2(2) - x, y)
(x' , y') = (4 - x, y) akan disubtitusi ke Step-2
Step-2 translasi (- 3, 4)
Translasi (a, b) dengan a = -3 dan b = 4.
(x", y") = (x' + (- 3), y' + 4)
(x", y") = (4 - x + (- 3), y + 4)
(x", y") = (1 - x, y + 4)
Sehingga, x" = 1 - x dan y" = y + 4
Setelah diatur dengan pindah ruas menjadi
Substitusikan ke bentuk awal x²+ y² = 4
⇔ (1 - x")² + (y" - 4)² = 4
Selanjutnya tanda aksen dapat dihilangkan
⇔ (1 - x)² + (y - 4)² = 4
⇔ x² - 2x + 1 + y² - 8y + 16 = 4
⇔ x² + y² - 2x - 8y + 1 + 16 - 4 = 0
Dari langkah-langkah pengerjaan di atas, diperoleh persamaan bayangan lingkaran
30. Pembahasan :
A(3,-2)
dipetakan oleh T(1 -2)
x' = x + 1 = 3 + 1 = 4
y' = y + (-2) = -2 + (-2) = -4
Bayangan A = A' = (4,-4)
lanjut rotasi [O , 90°]
x" = -y' = -(-4) = 4
y" = x' = 4
Bayangan akhir = A" = (4,4)
31. Pembahasan :

32. Pembahasan :
Koordinat (x, y) dicerminkan terhadap
sumbu X dilanjutkan dengan dilatasi
pusat O dan faktor skala 3, maka
Diperoleh
Substitusi persamaan (1) dan (2) ke persamaan kuadrat
Oleh karena itu, bayangan kurva y = x2 +
3x + 3 jika dicerminkan terhadap sumbu
X dilanjutkan dengan dilatasi pusat O dan
faktor skala 3 adalah
x² + 9x + 3y + 27 = 0
33. Pembahasan :
34. Pembahasan :
35. Pembahasan :
Bulan ke-2 = 55 rb
Bulan ke-3 = 60 rb
...
Bulan ke-24 (2 tahun) = ____?
Jumlah uang tabungan sampai 2 tahun, S24 = ___?
Jawab :
Deret aritmatika
Dengan :
U1 = a = 50 rb
Beda, b = 5 rb
U24 = ___?
Un = a + b(n - 1)
U24 = 50 rb + 5 rb(24 - 1)
U24 = 50 rb + 5 rb(23)
U24 = 50 rb + 115 rb
U24 = 165 rb
Jadi besar tabungan akhir saat 2 tahun adalah
Sn = n/2.(a + Un)
S24 = 24/2. (a + U24)
S24 = 12. (50 rb + 165 rb)
S24 = 12. (215 rb)
S24 = 2580 rb
Jadi uang akhir tabungannya sebesar
Rp. 2.580.000, 00
Diketahui :
- Harga beli (a) = Rp80.000.000
- Nilai jual (r) = 3/4
Ditanya : nilai jual setelah 3 tahun (U₄) = . . . ?
Jawab :
Nilai jual setelah 3 tahun adalah U₄ karena kita gunakan U₁ = 0 tahun.
Sehingga, nilai jual setelah dipakai 3 tahun
Kesimpulan : Jadi, harga jual mobil tersebut setelah dipakai 3 tahun adalah Rp33.750.000,00.
38. Pembahasan :
























Tidak ada komentar:
Posting Komentar