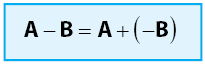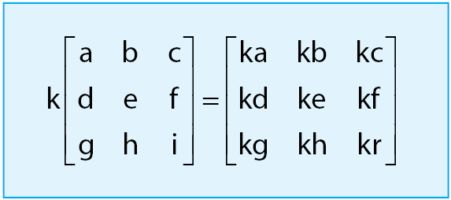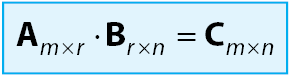Tugas matematika : Agustus 2020

Minggu, 30 Agustus 2020

MATRIKS

PENGERTIAN MATRIKS

Matriks adalah kumpulan bilangan yang disusun secara baris atau kolom atau kedua-duanya dan di dalam suatu tanda kurung. Bilangan-bilangan yang membentuk suatu matriks disebut sebagai elemen-elemen matriks. Matriks digunakan untuk menyederhanakan penyampaian data, sehingga mudah untuk diolah.

MACAM-MACAM MATRIKS

1. Matriks Baris dan Matriks Kolom

Matriks baris adalah suatu matriks yang hanya memiliki satu baris saja. Sedangkan, matriks kolom adalah suatu matriks yang hanya memiliki satu kolom saja. Contoh:

A = (1 4) atau B = (3 7 9) adalah matriks baris

$\begin{pmatrix} 146 \\ 275 \\ 528 \end{pmatrix}$ atau $D = \begin{pmatrix} p \\ q \end{pmatrix}$ adalah matriks kolom

2. Matriks Persegi

Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi. Matriks persegi memiliki ordo n.

Contoh: $A = \begin{pmatrix} 34 & 56 & 41 \\ 45 & 36 & 37 \\ 51 & 32 & 46 \end{pmatrix}$ adalah matriks persegi berordo 3, atau

atau

$B = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ adalah matriks persegi berordo 2.

3. Matriks Segitiga Atas dan Segitiga Bawah

Matriks persegi A yang memiliki elemen matriks $a_{ij} = 0$ untuk $i > j$ atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks $a_{ij} = 0$ untuk $i < j$ atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.

Contoh:

$A = \begin{pmatrix} 1 & 6 & 4 \\ 0 & 3 & 7 \\ 0 & 0 & 4 \end{pmatrix}$ adalah matriks segitiga atas,

$B = \begin{pmatrix} 1 & 0 & 0 \\ 7 & 3 & 0 \\ 4 & 6 & 4 \end{pmatrix}$ adalah matriks segitiga bawah.

4. Matriks Diagonal

Matriks persegi A yang memiliki elemen matiks $a_{ij} = 0$ untuk $i \neq j$ atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.

Contoh:

$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{pmatrix}$ atau $B = \begin{pmatrix} 1 & 0 \\ 0 & 4 \end{pmatrix}$

5. Matriks Skalar

Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.

Contoh:

$A = \begin{pmatrix} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{pmatrix}$ atau $B = \begin{pmatrix} 4 & 0 \\ 0 & 4 \end{pmatrix}$

6. Matriks Indentitas

Matriks identitas ialah matriks yang diagonal utamanya selalu bernilai 1. Contohnya sebagai berikut :

7. Matriks Simetris

Matriks persegi A yang memiliki elemen matiks baris ke-I sama dengan elemen matriks kolom ke-j untuk i = j disebut simetris. Atau, dapat dikatakan elemen $a_{ij}$ sama dengan elemen $a_{ji}$ .

Contoh:

$\begin{pmatrix} 1 & 2 & 4 \\ 2 & 3 & 5 \\ 4 & 5 & 7 \end{pmatrix}$

Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.

Transpose Matriks

Transpose matriks merupakan perubahan baris menjadi kolom dan sebaliknya. Transpose matriks dari $A_{m x n}$ adalah sebuah matriks dengan ukuran (n x m) dan bernotasi AT. Jika matriks A ditanspose, maka baris 1 menjadi kolom 1, baris 2 menjadi kolom 2, dan begitu seterusnya.

Contoh:

$\begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix}$ ditranspose menjadi $\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ .

Sifat dari transpose matriks: $(A^T)^T = A$ .

OPERASI MATRIKS

Penjumlahan Matriks

Operasi hitung matriks pada penjumlahan memiliki syarat yang harus dipenuhi agar dua buah matriks dapay dijumlahkan. Syarat dari dua buah matriks atau lebih dapat dijumlahkan jika memiliki nilai ordo yang sama. Artinya, semua matriks yang dijumlahkan harus memiliki jumlah baris dan kolom yang sama.

Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks dengan jumlah baris 3 dan kolom 4. Matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks dengan jumlah baris 4 dan kolom 3. Kesimpulannya, jumlah baris dan kolom antar dua matriks yang akan dijumlahkan harus sama.

Operasi hitung penjumlahan matriks memenuhi sifat komutatif, asosiatif, memiliki matriks identitas matriks nol, dan memiliki lawan matriks. Lawan matriks A adalah matriks $-A$ , di mana elemen-elemen matriks $-A$ merupakan lawan dari elemen-elemen matriks A. Secara ringkas, sifat operasi penjumlahan matriks dapat dilihat pada gambar di bawah

Sifat-sifat operasi penjumlahan matriks

Selanjutnya, kita akan mempelajari cara melakukan operasi hitung penjumlahan dua buah matriks. Penjelasan akan diberikan dalam bentuk contoh soal secara umum.

Contoh cara melakukan operasi penjumlahan pada matriks:

Pengurangan Matriks

Seperti halnya operasi hitung penjumlahan matriks, syarat agar dapat mengurangkan elemen-elemen antar matriks adalah matriks harus memiliki nilai ordo yang sama. Cara melakukan operasi pengurangan pada matriks dapat dilihat seperti cara di bawah.

Pengurangan Matriks

Cara melakukan operasi pengurangan dua matriks tidak jauh berbeda dengan penjumlahan matriks. Untuk lebih jelasnya, perhatikan contoh soal pengurangan matriks secara umum yang akan diberikan di bawah.

Contoh cara melakukan operasi pengurangan pada matriks:

Pengurangan Dua Matriks

Perkalian Matriks

Pembahasan operasi hitung matriks selanjutnya yang akan dibahas adalah perkalian matriks. Perkalian matriks yang akan dibahas di bawah adalah perkalian matriks dengan skalar dan perkalian matriks dengan matriks. Selengkapnya simak operasi hitung perkalian matriks di bawah.

Perkalian Matriks dengan Skalar

Cara melakukan operasi skalar pada matriks adalah dengan mengalikan semua elemen-elemen matriks dengan skalarnya. Jika k adalah suatu konstanta dan A adalah matriks, maka cara melakukan operasi perkalian skalar dapat dilihat melalui cara di bawah.

Perkalian Matriks dengan Skalar

Operasi Perkalian Dua Matriks

Perkalian Matriks

Operasi Hitung pada Matriks dan Sifat-sifatnya

CONTOH SOAL

2. Jika determinan nilai matriks A adalah 4 kali determinan nilai matriks B, maka nilai x adalah…

A. 4/3
B. 8/3
C. 10/4
D. 5/3
E. 16/7

Pembahasannya:
det A = 4 det B
4 x (16 x ) – (-16) = 4 (108 – (-152))
4 x (4 2x ) + 16 = 4 (260)
4 3x = 4 (260) – 16
4 3x = 4 (260) – 4 (4)
4 3x = 4 (260 – 4)
4 3x = 4 (256)
4 3x = 4. 4 4
4 3x = 4 5
3x = 5
x = 5/3

Jawabannya : D

DAFTAR PUSTAKA

https://www.studiobelajar.com/matriks-dasar/

https://idschool.net/sma/operasi-hitung-penjumlahan-pengurangan-perkalian-matriks/

https://rumus.waheedbaly.com/contoh-soal-matriks-dan-jawabannya-kelas-11/

Minggu, 23 Agustus 2020

SOAL CERITA UNTUK MENENTUKAN NILAI OPTIMUM

Soal :

Dengan persediaan kain polos 20 m dan kain bergaris 10 m, Dewi akan membuat 2 model pakaian jadi. Model I memerlukan tidak lebih dari 1 m kain polos dan 1,5 m kain bergaris. Model II memerlukan tidak lebih dari 2 m kain polos dan 0,5 m kain bergaris. Bila pakaian tersebut dijual, setiap model I memperoleh untung tidak kurang dari Rp. 15.000,00 dan model II memperoleh untung tidak kurang dari Rp. 10.000,00. Laba yang diperoleh Dewi adalah sebanyak ...

Jawab :

MENENTUKAN NILAI OPTIMUM

soal cerita dan penyelesaiannya yang terkait dengan nilai optimum proram linear :

contoh 1.

Untuk memproduksi sepeda jenis A dengan harga jual Rp.600.000 suatu perusahaan membutuhkan biaya Rp. 200.000 dan waktu 20 jam. Sedangkan sepeda jenis B dengan harga jual Rp. 800.000 membutuhkan biaya Rp. 100.000 dengan waktu 30 jam. Jika dana yang tersedia Rp. 1.200.000 dan waktu kerja 240 jam per bulan, maka tentukanlah hasil penjualan maksimum yang diperoleh tiap bulan

Jawab
Misalkan
x = banyaknya sepeda jenis A
y = banyaknya sepeda jenis B
maka dapat disusun kendala biaya dan waktu produksi sebagai berikut:
200000x + 100000y ≤ 1200000
20x + 30y ≤ 240
x ≥ 0
y ≥ 0
Jika disederhanakan menjadi :
2x + y ≤ 12
2x + 3y ≤ 24
x ≥ 0

y ≥ 0
Fungsi penjualan : f(x, y) = 600000x + 800000y
Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

Titik A koordinatnya adalah A(0, 8)
Titik C koordinatnya adalah C(6, 0)
Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

karena 2x + y = 12 maka 2x + 6 = 12, sehingga 2x = 6, jadi x = 3
Jadi koordinat titik B adalah B(3, 6)
Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 600000x + 800000y, sehingga diperoleh :
A(0, 8) → f(A) = 600000(0) + 800000(8) = 6.400.000
B(6, 2) → f(B) = 600000(6) + 800000(2) = 5.200.000
C(3, 6) → f(C) = 600000(3) + 800000(6) = 6.600.000
Jadi hasil penjualan maksimum yang diperoleh tiap bulan adalah Rp. 6.600.000

contoh 2.

Seorang anak diharuskan memakan dua jenis tablet tiap hari. Tablet pertama mengandung 2 unit vitamin A dan 2 unit vitamin B, sedangkan tablet kedua mengandung 3 unit vitamin A dan 1 unit vitamin B. Dalam satu hari anak itu memerlukan paling sedikit 12 unit vitamin A dan 8 unit vitamin B. Jika harga tablet pertama Rp. 500 perbutir dan tablet kedua Rp. 1.000 perbutir maka agar pengeluaran minimum banyak tablet pertama yang harus dibeli adalah …

Jawab
Misalkan x = banyaknya tablet jenis pertama
y = banyaknya tablet jenis kedua
maka dapat disusun kendala kebutuhan vitamin A dan vitamin B sebagai berikut:

Dari tabel di atas dapat disusun kendala, yakni :
2x + 3y ≥ 12

2x + y ≥ 8
x ≥ 0
y ≥ 0
Fungsi pengeluaran f(x, y) = 500x + 1000y
Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

Titik A koordinatnya adalah A(0, 8)
Titik C koordinatnya adalah C(6, 0)
Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

karena 2x + y = 8 maka 2x + 2 = 8, sehingga 2x = 6 , x =3

Jadi koordinat titik B adalah B(3, 2)
Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 500x + 1000y, sehingga diperoleh :
A(0, 8) → f(A) = 500(0) + 1000(8) = 8.000
B(3, 2) → f(B) = 500(3) + 1000(2) = 3.500
C(6, 0) → f(C) = 500(6) + 1000(0) = 3.000
Jadi besarnya pengeluaran minimum Rp. 3.000 didapat jika dibeli 6 tablet pertama

contoh 3.

Seorang pedagang minuman menjual dua jenis minuman ringan pada suatu tempat yang dapat menampung 500 botol minuman. Harga beli minuman jenis A dan jenis B masing-masing Rp. 2000 dan Rp 4000 per botol. Jika ia memiliki modal Rp. 1.600.000 serta akan memperoleh laba perbuah Rp. 800 untuk minuman jenis A dan Rp. 600 untuk minuman jenis B, maka berapakah banyaknya minuman minuman jenis A dan B agar diperoleh laba maksimum ?

Jawab
Misalkan
x = banyaknya minuman jenis A
y = banyaknya minuman jenis B
maka dapat disusun kendala modal dan kapasitas kios sebagai berikut:
x + y ≤ 500
2000x + 4000y ≤ 1.600.000
x ≥ 0
y ≥ 0
Jika disederhanakan menjadi :
x + y ≤ 500
x + 2y ≤ 800
x ≥ 0
y ≥ 0
Fungsi laba : f(x, y) = 800x + 600y
Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

Titik A koordinatnya adalah A(0, 400)
Titik C koordinatnya adalah C(500, 0)
Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

karena x + y = 500 maka x + 300 = 500, sehingga x = 200
Jadi koordinat titik B adalah B(200, 300)
Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 800x + 600y, sehingga diperoleh :
A(0, 400) → f(A) = 800(0) + 600(400) = 240.000
B(200, 300) → f(B) = 800(200) + 600(300) = 360.000
C(500, 0) → f(C) = 800(500) + 600(0) = 400.000
Jadi keuntungan maksimum yakni sebesar Rp. 400.000 diperoleh jika dijual minuman jenis A saja sebanyak 500 botol

contoh 4.

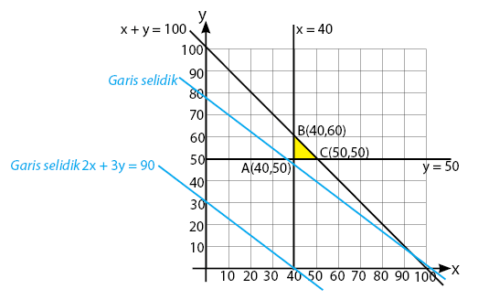
Luas daerah parkir 1.760 m² . Luas rata-rata untuk mobil kecil 4 m² dan mobil besar 20 m² . Daya tampung maksimum hanya 200 kendaraan, biaya parker mobil kecil Rp. 1000/jam dan mobil besar Rp.2000/jam. Jika dalam satu jam terisi penuh dan tidak ada kendaraan yang pergi dan dating, maka hasil maksimum tempat parkir itu adalah:

A. Rp.176.000,-

B. Rp. 200.000,-

C. Rp.260.000,-

D. Rp. 300.000,-

E. Rp.340.000,-

Jawaban : C

Pembahasan :

Dibuat persamaan-persamaannya terlebih dahulu:

Misal mobil kecil = x dan mobil besar = y

4 x + 20 y ≤ 1760

x + 5y ≤ 440 …..(1)

x + y ≤ 200 ….(2)

nilai maksimum 1000x + 2000y = ?

buat sketsa grafiknya:

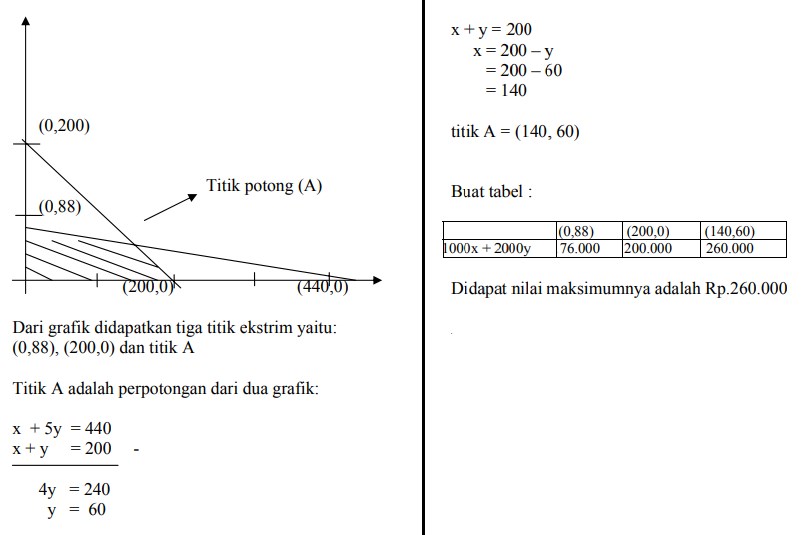
soal program linear dan jawaban no 11

contoh 5.

Seorang tukang roti mempunyai bahan A,B dan C masing-masing sebanyak 160 kg, 110 kg dan 150 kg.

Roti I memerlukan 2 kg bahan A, 1 kg bahan B dan 1 Kg bahan C
Roti II memerlukan 1 kg bahan A, 2 kg bahan B dan 3 Kg bahan C

Sebuah roti I dijual dengan harga Rp.30.000 dan sebuah roti II dijual dengan harga Rp.50.000, pendapatan maksimum yang dpat diperoleh tukang roti tersebut adalah…

A. Rp. 8000.000,-

B. Rp. 4500.000,-

C. Rp. 3900.000,-

D. Rp. 3100.000,-

E. Rp. 2900.000,-

Jawaban : D

Pembahasan :

Buat persamaan :

Misal roti I = x dan roti II = y didapat persamaan sbb:

2x + y ≤ 160 …..(1)
x + 2y ≤ 110 …..(2)
x + 3y ≤ 150 ….(3)

buat sketsa grafiknya:

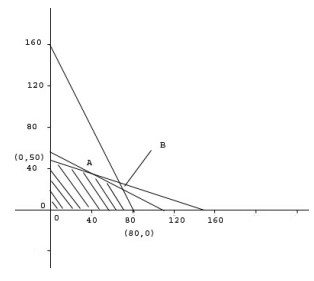
soal program linear dan jawaban no 10

Daerah yang diarsir adalah himpunan penyelesaian dari tiga grafik tsb. Didapat 4 titik ekstrim yaitu (0,50), (80,0), titik A dan titik B

perpotongan (1) dan (2) → titik B

soal program linear dan jawaban no 10-1

contoh 6.

Pedagang buah memiliki modal Rp. 1.000.000,00 untuk membeli apel dan pisang untuk dijual kembali. Harga beli tiap kg apel Rp 4000,00 dan pisang Rp 1.600,00. Tempatnya hanya bisa menampung 400 kg buah. Tentukan jumlah apel dan pisang agar kapasitas maksimum.

Pembahasan 3:

Diketahui:

contoh soal model matematika

Dengan syarat:

Kapasitas tempat: x + y ≤ 400
Modal: 4.000x + 1.600y ≤ 1.000.000 $5x + 2y \le 1.250$
x ≥ 0
y ≥ 0

Diagramnya:

Titik ekstrim:

A(0, 400) bukan optimum karena tidak ada apel
C(250, 0) bukan optimum karena tidak ada pisang
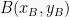$B(x_B, y_B)$ dengan metode eliminasi 2 persamaan diatas diperoleh:

Sehingga jumlah masimum:

Apel: 150 kg
Pisang: 250 kg.

contoh 7.

Uang Adinda Rp 40.000,00 lebih banyak dari uang Binary ditambah dua kali uang Cindy. Jumlah uang Adinda, Binary, dan Cindy Rp 200.000. Selisih uang Binary dan Cindy Rp 10.000,00. Jumlah uang Adinda dan Binary adalah ...

Rp 122.000,00
Rp 126.000,00
Rp 156.000,00
Rp 162.000,00
Rp 172.000,00

Pembahasan :
Kita lakukan pemisalan :

Adinda = a
Binary = b
Cindy =c

Karena ada tiga variabel, maka persamaan yang kita bentuk adalah persamaan linear tiga variabel. Ada tiga persamaan yang kita peroleh dari soal yaitu :
(1) a = 40.000 + b + 2c → a - b - 2c = 40.000
(2) a + b + c = 200.000
(3) b - c = 10.000

Dari persamaan (1) ke (2) :

a - b - 2c = 40.000

a + b + c = 200.000 -

-2b - 3c = -160.000 ......(4)

Dari persamaan (3) dan (4) :

b - c = 10.000 |x3

-2b - 3c = -160.000 |x1

3b - 3c = 30.000

-2b - 3c = -160.000 -

5b = 190.000

b = 38.000

Selanjutnya substitusi b = 38.000 ke persamaan (3) :
⇒ b - c = 10.000
⇒ 38.000 - c = 10.000
⇒ c = 28.000

Pada soal ditanya jumlah uang Adinda dan Binary (a + b) Nilai c sudah kita peroleh, maka dari persamaan (2) kita peroleh :
⇒ a + b + c = 200.000
⇒ a + b = 200.000 - c
⇒ a + b = 200.000 - 28.000
⇒ a + b = 172.000
Jadi jumlah uang Adinda dan Binary adalah Rp 172.000,00

contoh 8.

Harga 2 kg mangga, 2kg jeruk, dan 1 kg anggur adalah Rp 70.000,00. Harga 1 kg mangga, 2 kg jeruk, dan 2 kg anggur adalah Rp 90.000,00. Jika harga 2 kg mangga, 2kg jeruk, dan 3 kg anggur Rp 130.000,00, maka harga 1 kg jeruk adalah ....

Rp 5.000,00
Rp 7.500,00
Rp 10.000,00
Rp 12.000,00
Rp 15.000,00

Pembahasan :
Kita lakukan pemisalan :

Mangga = x
Jeruk = y
Anggur = z

Karena ada tiga variabel, maka persamaan yang kita bentuk adalah persamaan linear tiga variabel. Ada tiga persamaan yang kita peroleh dari soal yaitu :
(1) 2x + 2y + z = 70.000
(2) x + 2y + 2z = 90.000
(3) 2x + 2y + 3z = 130.000

Dari persamaan (1) dan (2) :

2x + 2y + z = 70.000 |x1

x + 2y + 2z = 90.000 |x2

2x + 2y + z = 70.000

2x + 4y + 4z = 180.000 -

-2y - 3z = -110.000 ......(4)

Dari persamaan (2) dan (3) :

x + 2y + 2z = 90.000 |x2

2x + 2y + 3z = 130.000 |x1

2x + 4y + 4z = 180.000

2x + 2y + 3z = 130.000 -

2y + z = 50.000 ......(5)

Ingat bahwa kita mau mencari harga jeruk (y) maka yang harus kita eliminasi selanjutnya adalah z.
Dari persamaan (4) dan (5) :

-2y - 3z = -110.000 |x1

2y + z = 50.000 |x3

-2y - 3z = -110.000

6y + 3z = 150.000 +

4y = 40.000

y = 10.000

Jadi, harga 1 kg jeruk adalah Rp 10.00,00

contoh 9. .

Luas daerah parkir 360 m2. Luas rata-rata sebuah mobil 6 m2 dan luas rata – rata bus 24 m2. Daerah parkir tersebut dapat memuat paling banyak 30 kendaraan roda empat (mobil dan bus). Jika tarif parkir mobil Rp2.000,00 dan tarif parkir bus Rp5.000,00 maka pendapatan terbesar yang dapat diperoleh adalah ….

Pembahasannya

Misalkan:

x = banyak mobil
y = banyak bus

Perhatikan tabel di bawah!

Pembahasannya

Misalkan:

x = banyak mobil
y = banyak bus

Perhatikan tabel di bawah!

Pembahasannya

Misalkan:

x = banyak mobil
y = banyak bus

Perhatikan tabel di bawah!

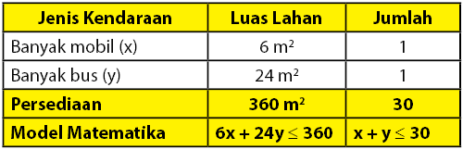
Pemodelan Matematika pada Program Linear

Diperoleh dua persamaan:

x + y ≤ 30
6x + 24y ≤ 360 → x + 4y ≤ 60

Menentukan daerah yang memenuhi pertidaksamaan:

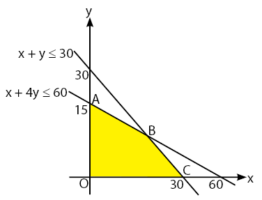
Contoh Soal Ujian Nasional Program Linear

Akan ditentukan nilai maksimum dengan metode titik sudut.

Titik koordinat O, A, dan C dapat diperoleh dengan melihat gambar, yaitu O(0,0), A(0, 15), dan C(30,0). Untuk koordinat B dapat diperoleh dengan menggunakan eliminasi dan substitusi.

Metode eliminasi

Substitusi nilai y = 10 pada persamaan x + y = 30 untuk mendapatkan nilai x.

x + y = 30
x + 10 = 30
x = 30 – 10 = 20

Koordinat titik B adalah (20, 10)

Perhitungan keuntungan maksimal yang dapat diperoleh:

Fungsi Objektif Pembahasan Soal Ujian Nasional Program Linear SMA

Jawaban: E

contoh 10.

Biaya produksi satu buah payung jenis A adalah Rp20.000,00 per buah, sedangkan biaya satu buah produksi payung jenis B adalah Rp30.000,00. Seorang pengusaha akan membuat payung A dengan jumlah tidak kurang dari 40 buah. Sedangkan banyaknya payung jenis B yang akan diproduksi minimal adalah dari 50 buah. Jumlah maksimal produksi kedua payung tersebut adalah 100 buah. Biaya minimum yang dikeluarkan untuk melakukan produksi kedua payung sesuai ketentuan tersebut adalah ….

A. Rp2.000.000,00
B. Rp2.300.000,00
C. Rp2.200.000,00
D. Rp2.100.000,00
E. Rp2.000.000,00

Pembahasan:

Pemisalan:

x = banyak payung A
y = banyak payung B

Model matematika dari permasalahan tersebut adalah:

Fungsi tujuan: meminimumkan f(x,y) = 20.000x + 30.000y

Fungsi kendala:

x ≥ 40
y ≥ 50
x + y ≤ 100

Daerah penyelesaian yang memenuhi permasalahan:

Daerah Penyelesaian Metode Garis Selidik

Nilai minimum akan diperoleh melalui titik koordinat yang dilalui garis selidik yang pertama kali, yaitu titik A(40, 50).

Sehingga, biaya produksi minimum adalah

f(40,50) = 20.000(40) + 30.000(50)
f(40,50) = 800.000 + 1.500.000
f(40,50) = 2.300.000

Jawaban: B

daftar pustaka :

https://www.materimatematika.com/2017/10/menafsirkan-nilai-optimum-dalam-program.html

https://www.studiobelajar.com/program-linear/

https://idschool.net/sma/contoh-soal-dan-pembahasan-program-linear-matematika-sma/

https://soalkimia.com/contoh-soal-program-linear/

Tugas matematika

Minggu, 30 Agustus 2020

MATRIKS

1. Matriks Baris dan Matriks Kolom

2. Matriks Persegi

3. Matriks Segitiga Atas dan Segitiga Bawah

4. Matriks Diagonal

5. Matriks Skalar

6. Matriks Indentitas

7. Matriks Simetris

Transpose Matriks

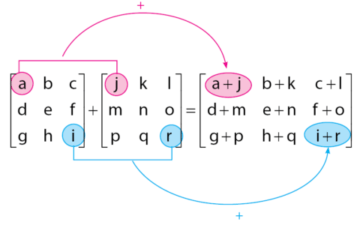
Penjumlahan Matriks

Pengurangan Matriks

Perkalian Matriks

Minggu, 23 Agustus 2020

SOAL CERITA UNTUK MENENTUKAN NILAI OPTIMUM

MENENTUKAN NILAI OPTIMUM

pembelajaran online

Laporkan Penyalahgunaan