soal cerita dan penyelesaiannya yang terkait dengan nilai optimum proram linear :
contoh 1.
Untuk memproduksi sepeda jenis A dengan harga jual Rp.600.000 suatu perusahaan membutuhkan biaya Rp. 200.000 dan waktu 20 jam. Sedangkan sepeda jenis B dengan harga jual Rp. 800.000 membutuhkan biaya Rp. 100.000 dengan waktu 30 jam. Jika dana yang tersedia Rp. 1.200.000 dan waktu kerja 240 jam per bulan, maka tentukanlah hasil penjualan maksimum yang diperoleh tiap bulan
Jawab
Misalkan
x = banyaknya sepeda jenis A
y = banyaknya sepeda jenis B
maka dapat disusun kendala biaya dan waktu produksi sebagai berikut:
200000x + 100000y ≤ 1200000
20x + 30y ≤ 240
x ≥ 0
y ≥ 0
Jika disederhanakan menjadi :
2x + y ≤ 12
2x + 3y ≤ 24
x ≥ 0
y ≥ 0
Fungsi penjualan : f(x, y) = 600000x + 800000y
Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas
Titik A koordinatnya adalah A(0, 8)
Titik C koordinatnya adalah C(6, 0)
Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :
karena 2x + y = 12 maka 2x + 6 = 12, sehingga 2x = 6, jadi x = 3
Jadi koordinat titik B adalah B(3, 6)
Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 600000x + 800000y, sehingga diperoleh :
A(0, 8) → f(A) = 600000(0) + 800000(8) = 6.400.000
B(6, 2) → f(B) = 600000(6) + 800000(2) = 5.200.000
C(3, 6) → f(C) = 600000(3) + 800000(6) = 6.600.000
Jadi hasil penjualan maksimum yang diperoleh tiap bulan adalah Rp. 6.600.000
contoh 2.
Seorang anak diharuskan memakan dua jenis tablet tiap hari. Tablet pertama mengandung 2 unit vitamin A dan 2 unit vitamin B, sedangkan tablet kedua mengandung 3 unit vitamin A dan 1 unit vitamin B. Dalam satu hari anak itu memerlukan paling sedikit 12 unit vitamin A dan 8 unit vitamin B. Jika harga tablet pertama Rp. 500 perbutir dan tablet kedua Rp. 1.000 perbutir maka agar pengeluaran minimum banyak tablet pertama yang harus dibeli adalah …
Jawab
Misalkan x = banyaknya tablet jenis pertama
y = banyaknya tablet jenis kedua
maka dapat disusun kendala kebutuhan vitamin A dan vitamin B sebagai berikut:

2x + 3y ≥ 12
x ≥ 0
y ≥ 0
Fungsi pengeluaran f(x, y) = 500x + 1000y
Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

Titik C koordinatnya adalah C(6, 0)
Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 500x + 1000y, sehingga diperoleh :
A(0, 8) → f(A) = 500(0) + 1000(8) = 8.000
B(3, 2) → f(B) = 500(3) + 1000(2) = 3.500
C(6, 0) → f(C) = 500(6) + 1000(0) = 3.000
Jadi besarnya pengeluaran minimum Rp. 3.000 didapat jika dibeli 6 tablet pertama
Jawab
Misalkan
x = banyaknya minuman jenis A
y = banyaknya minuman jenis B
maka dapat disusun kendala modal dan kapasitas kios sebagai berikut:
x + y ≤ 500
2000x + 4000y ≤ 1.600.000
x ≥ 0
y ≥ 0
Jika disederhanakan menjadi :
x + y ≤ 500
x + 2y ≤ 800
x ≥ 0
y ≥ 0
Fungsi laba : f(x, y) = 800x + 600y
Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

Titik C koordinatnya adalah C(500, 0)
Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

Jadi koordinat titik B adalah B(200, 300)
Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 800x + 600y, sehingga diperoleh :
A(0, 400) → f(A) = 800(0) + 600(400) = 240.000
B(200, 300) → f(B) = 800(200) + 600(300) = 360.000
C(500, 0) → f(C) = 800(500) + 600(0) = 400.000
Jadi keuntungan maksimum yakni sebesar Rp. 400.000 diperoleh jika dijual minuman jenis A saja sebanyak 500 botol
A. Rp.176.000,-
B. Rp. 200.000,-
C. Rp.260.000,-
D. Rp. 300.000,-
E. Rp.340.000,-
Jawaban : C
Pembahasan :
Dibuat persamaan-persamaannya terlebih dahulu:
Misal mobil kecil = x dan mobil besar = y
4 x + 20 y ≤ 1760
x + 5y ≤ 440 …..(1)
x + y ≤ 200 ….(2)
nilai maksimum 1000x + 2000y = ?
buat sketsa grafiknya:
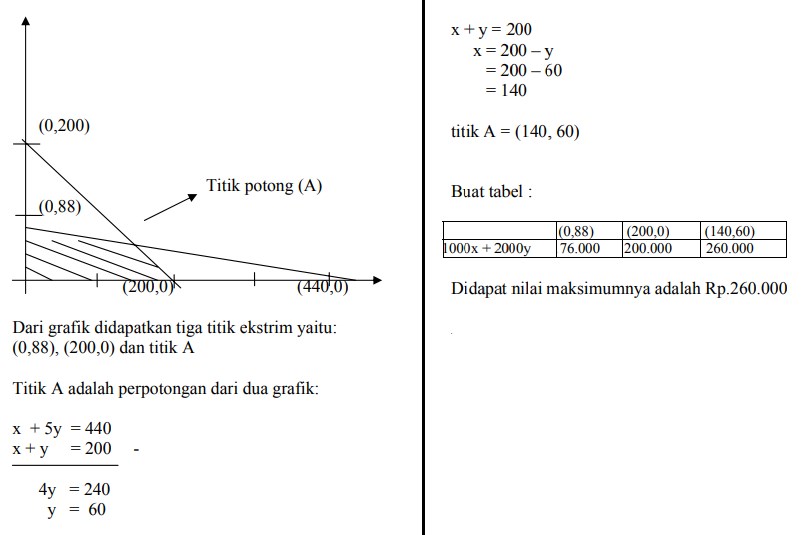
contoh 5.
Seorang tukang roti mempunyai bahan A,B dan C masing-masing sebanyak 160 kg, 110 kg dan 150 kg.
- Roti I memerlukan 2 kg bahan A, 1 kg bahan B dan 1 Kg bahan C
- Roti II memerlukan 1 kg bahan A, 2 kg bahan B dan 3 Kg bahan C
Sebuah roti I dijual dengan harga Rp.30.000 dan sebuah roti II dijual dengan harga Rp.50.000, pendapatan maksimum yang dpat diperoleh tukang roti tersebut adalah…
A. Rp. 8000.000,-
B. Rp. 4500.000,-
C. Rp. 3900.000,-
D. Rp. 3100.000,-
E. Rp. 2900.000,-
Jawaban : D
Pembahasan :
Buat persamaan :
Misal roti I = x dan roti II = y didapat persamaan sbb:
- 2x + y ≤ 160 …..(1)
- x + 2y ≤ 110 …..(2)
- x + 3y ≤ 150 ….(3)
buat sketsa grafiknya:
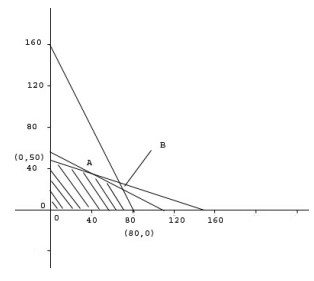
Daerah yang diarsir adalah himpunan penyelesaian dari tiga grafik tsb. Didapat 4 titik ekstrim yaitu (0,50), (80,0), titik A dan titik B
perpotongan (1) dan (2) → titik B

contoh 6.
Pedagang buah memiliki modal Rp. 1.000.000,00 untuk membeli apel dan pisang untuk dijual kembali. Harga beli tiap kg apel Rp 4000,00 dan pisang Rp 1.600,00. Tempatnya hanya bisa menampung 400 kg buah. Tentukan jumlah apel dan pisang agar kapasitas maksimum.
Pembahasan 3:
Diketahui:

Dengan syarat:
- Kapasitas tempat: x + y ≤ 400
- Modal: 4.000x + 1.600y ≤ 1.000.000
- x ≥ 0
- y ≥ 0
Diagramnya:

Titik ekstrim:
- A(0, 400) bukan optimum karena tidak ada apel
- C(250, 0) bukan optimum karena tidak ada pisang
dengan metode eliminasi 2 persamaan diatas diperoleh:

Sehingga jumlah masimum:
- Apel: 150 kg
- Pisang: 250 kg.
|
Pembahasan :
Kita lakukan pemisalan :
- Adinda = a
- Binary = b
- Cindy =c
Karena ada tiga variabel, maka persamaan yang kita bentuk adalah persamaan linear tiga variabel. Ada tiga persamaan yang kita peroleh dari soal yaitu :
(1) a = 40.000 + b + 2c → a - b - 2c = 40.000
(2) a + b + c = 200.000
(3) b - c = 10.000
Dari persamaan (1) ke (2) :
| a - b - 2c = 40.000 |
| a + b + c = 200.000 - |
| -2b - 3c = -160.000 ......(4) |
Dari persamaan (3) dan (4) :
| b - c = 10.000 |x3 |
| -2b - 3c = -160.000 |x1 |
| 3b - 3c = 30.000 |
| -2b - 3c = -160.000 - |
| 5b = 190.000 |
| b = 38.000 |
Selanjutnya substitusi b = 38.000 ke persamaan (3) :
⇒ b - c = 10.000
⇒ 38.000 - c = 10.000
⇒ c = 28.000
Pada soal ditanya jumlah uang Adinda dan Binary (a + b) Nilai c sudah kita peroleh, maka dari persamaan (2) kita peroleh :
⇒ a + b + c = 200.000
⇒ a + b = 200.000 - c
⇒ a + b = 200.000 - 28.000
⇒ a + b = 172.000
Jadi jumlah uang Adinda dan Binary adalah Rp 172.000,00
|
Pembahasan :
Kita lakukan pemisalan :
- Mangga = x
- Jeruk = y
- Anggur = z
Karena ada tiga variabel, maka persamaan yang kita bentuk adalah persamaan linear tiga variabel. Ada tiga persamaan yang kita peroleh dari soal yaitu :
(1) 2x + 2y + z = 70.000
(2) x + 2y + 2z = 90.000
(3) 2x + 2y + 3z = 130.000
Dari persamaan (1) dan (2) :
| 2x + 2y + z = 70.000 |x1 |
| x + 2y + 2z = 90.000 |x2 |
| 2x + 2y + z = 70.000 |
| 2x + 4y + 4z = 180.000 - |
| -2y - 3z = -110.000 ......(4) |
Dari persamaan (2) dan (3) :
| x + 2y + 2z = 90.000 |x2 |
| 2x + 2y + 3z = 130.000 |x1 |
| 2x + 4y + 4z = 180.000 |
| 2x + 2y + 3z = 130.000 - |
| 2y + z = 50.000 ......(5) |
Ingat bahwa kita mau mencari harga jeruk (y) maka yang harus kita eliminasi selanjutnya adalah z.
Dari persamaan (4) dan (5) :
| -2y - 3z = -110.000 |x1 |
| 2y + z = 50.000 |x3 |
| -2y - 3z = -110.000 |
| 6y + 3z = 150.000 + |
| 4y = 40.000 |
| y = 10.000 |
Jadi, harga 1 kg jeruk adalah Rp 10.00,00
- x = banyak mobil
- y = banyak bus
Perhatikan tabel di bawah!
- x = banyak mobil
- y = banyak bus
Perhatikan tabel di bawah!
- x = banyak mobil
- y = banyak bus
Perhatikan tabel di bawah!
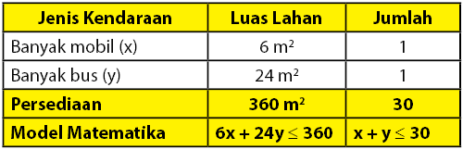
Diperoleh dua persamaan:
- x + y ≤ 30
- 6x + 24y ≤ 360 → x + 4y ≤ 60
Menentukan daerah yang memenuhi pertidaksamaan:
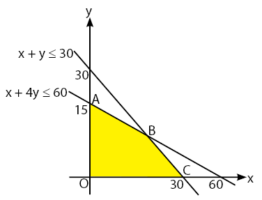
Akan ditentukan nilai maksimum dengan metode titik sudut.
Titik koordinat O, A, dan C dapat diperoleh dengan melihat gambar, yaitu O(0,0), A(0, 15), dan C(30,0). Untuk koordinat B dapat diperoleh dengan menggunakan eliminasi dan substitusi.

Substitusi nilai y = 10 pada persamaan x + y = 30 untuk mendapatkan nilai x.
x + y = 30
x + 10 = 30
x = 30 – 10 = 20
Koordinat titik B adalah (20, 10)
Perhitungan keuntungan maksimal yang dapat diperoleh:

Jawaban: E
contoh 10.
Biaya produksi satu buah payung jenis A adalah Rp20.000,00 per buah, sedangkan biaya satu buah produksi payung jenis B adalah Rp30.000,00. Seorang pengusaha akan membuat payung A dengan jumlah tidak kurang dari 40 buah. Sedangkan banyaknya payung jenis B yang akan diproduksi minimal adalah dari 50 buah. Jumlah maksimal produksi kedua payung tersebut adalah 100 buah. Biaya minimum yang dikeluarkan untuk melakukan produksi kedua payung sesuai ketentuan tersebut adalah ….
A. Rp2.000.000,00
B. Rp2.300.000,00
C. Rp2.200.000,00
D. Rp2.100.000,00
E. Rp2.000.000,00
Pembahasan:
Pemisalan:
- x = banyak payung A
- y = banyak payung B
Model matematika dari permasalahan tersebut adalah:
Fungsi tujuan: meminimumkan f(x,y) = 20.000x + 30.000y
Fungsi kendala:
- x ≥ 40
- y ≥ 50
- x + y ≤ 100
Daerah penyelesaian yang memenuhi permasalahan:
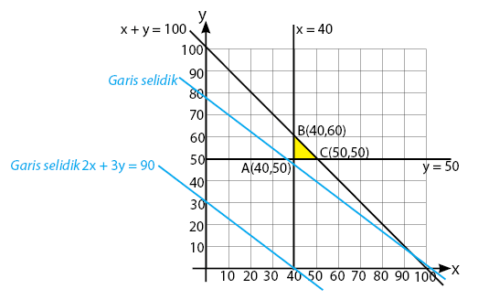
Nilai minimum akan diperoleh melalui titik koordinat yang dilalui garis selidik yang pertama kali, yaitu titik A(40, 50).
Sehingga, biaya produksi minimum adalah
f(40,50) = 20.000(40) + 30.000(50)
f(40,50) = 800.000 + 1.500.000
f(40,50) = 2.300.000
Jawaban: B
daftar pustaka :
https://www.materimatematika.com/2017/10/menafsirkan-nilai-optimum-dalam-program.html
https://www.studiobelajar.com/program-linear/
https://idschool.net/sma/contoh-soal-dan-pembahasan-program-linear-matematika-sma/


Tidak ada komentar:
Posting Komentar