nama : tabitha fransisca r.n
kelas : xi ips 3
absen 35
Barisan geometri merupakan barisan yang memenuhi sifat hasil bagi sebuah suku dengan suku sebelumnya yang berurutan. Nah, hal tersebut bernilai konstan. Selain itu, barisan geometri juga sering diistilahkan sebagai “barisan ukur”. barisan deret geometri ini masih berhubungan dengan barisan dan deret aritmatika
Rumus Mencari Rasio

Kalau kamu sudah mengetahui  dan
dan  nya, sekarang kita pelajari rumus suku ke – n (
nya, sekarang kita pelajari rumus suku ke – n ( ) dan juga rumus jumlah n suku yang pertama (
) dan juga rumus jumlah n suku yang pertama ( )
)
Rumus Mencari Un
Untuk mencari suku ke n pada barisan dan deret geometri, kamu bisa menggunakan rumus berikut ini

Misalnya kita punya barisan dan deret
Syaratnya adalah kamu mengetahui berapa  nya dan berapa
nya dan berapa
 nya. Dengan begitu kamu sudah bisa mencari
nya. Dengan begitu kamu sudah bisa mencari  dengan mudah.
dengan mudah.
Rumus Mencari Sn
 adalah jumlah suku ke n pada barisan dan deret. Nah bagaimana cara kita mencari tau
adalah jumlah suku ke n pada barisan dan deret. Nah bagaimana cara kita mencari tau  pada barisan dan deret geometri? Di bawah ini adalah rumusnya.
pada barisan dan deret geometri? Di bawah ini adalah rumusnya.
Misalnya kita punya barisan dan deret
 dst. Nah itu adalah cara kita mengetahui berapa S1, S2, S3, dan seterusnya.
dst. Nah itu adalah cara kita mengetahui berapa S1, S2, S3, dan seterusnya.
Selanjutnya di bawah ini adalah rumus mencari  .
.

contoh soal
BARISAN
1.
- Ada Sebuah barisan geometri yang untuk mencari suku Un.cari dan hitunglah suku Un yang ke 10 dari barisan 1/8, 1/4, 1/2,…. tersebut !
Penyelesaian :
Diketahui :
- = r = 1/4 : 1/8 = 1/4 x 8 = 2 (rasionya)
Jawab :
- Un = arn – 1
- Un = 1/8 . 2 (10 – 1) = 1/8 . 29 = 2 – 3 . 29 = 26 = 64
Jadi, suku Un yang ke 10 tersebut adalah = 64
2. Ada Sebuah amoeba membelah diri menjadi 2 setiap 6 menit,berapakah jumlah amoeba setelah satu jam jika awalnya terdapat hanya 2 amoeba .cari dan hitunglah suku Un jumlah amoeba tersebut !
Penyelesaian :
Diketahui :
- a = 2
- r = 2
- n = (1 jam/6 menit) + 1 = 11
Jawab :
- Un = arn – 1
- Un = 2 . 2 11 – 1 = 210 = 1024 buah amoeba
Jadi, suku Un untuk mencari amoeba tersebut adalah = 1024 buah amoeba
3. Ada Sebuah barisan geometri yang untuk mencari suku Un.cari dan hitunglah suku Un yang ke 7 dari barisan 3, 6, 2,…. tersebut !
Penyelesaian :
Diketahui :
Jawab :
- Un = ar(n-1)
- Un = 3.2(7-1)
- U7 = 3.2(7-1)
- U7 = 192
Jadi, suku Un yang ke 17 tersebut adalah = 192
4. Ada Sebuah barisan geometri yang untuk mencari suku Un.cari dan hitunglah suku Un yang ke 7 dari barisan 48, 24, 12,…. tersebut !
Penyelesaian :
Diketahui :
Jawab :
- Un = arn-1
- Un = 48.(1/2)n-1
- Un = 48.(1/2)n-1
- Un = 48.(2-1)1-n
- Un = 3.16. (2)1-n
- U7 = 3.24 (2)1-n
- U7 = 3.25-n
Jadi, suku Un yang ke 7 tersebut adalah = 3.25-n
5. Ada Sebuah barisan geometri yang untuk mencari suku Un.cari dan hitunglah suku Un yang ke 7 dari barisan 44, 24, 12,…. tersebut !
Penyelesaian :
Diketahui :
Jawab :
- Un = arn-1
- Un = 44.(1/2)n-1
- Un = 44.(1/2)n-1
- Un = 44.(2-1)1-n
- Un = 3.8. (2)1-n
- U7 = 3.23 (2)1-n
- U7 = 3.24-n
6. Selembar kertas dipotong menjadi dua bagian. Setiap bagian dipotong menjadi dua dan seterusnya. Jumlah potongan kertas setelah potongan kelima sama dengan …
Pembahasan:
Diketahui: a = 1
r = 2
Ditanya: 
Jawab:


=32
Jadi, jumlah potongan kertas setelah potongan kelima adalah 32
7. Diketahui suku ke-5 dari barisan geometri adalah 243, hasil bagi suku ke-9 dengan suku ke-6 adalah 27. Suku ke-2 dari barisan tersebut adalah …
Pembahasan:
Diketahui 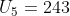
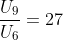
Ditanya 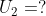
Jawab:
Sebelum kita mencari nilai dari 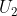 , kita akan mencari nilai a dan r terlebih dahulu.
, kita akan mencari nilai a dan r terlebih dahulu.
Ingat kembali 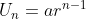 maka
maka
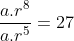
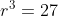
![r=\sqrt[3]{27}](https://latex.codecogs.com/gif.latex?r=\sqrt[3]{27})
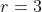
Substitusikan r = 3 ke persamaan 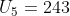
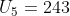
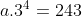
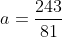
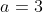
sehingga
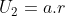
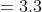
= 9
Jadi, suku ke-2 dari barisan tersebut adalah 9.
DERET
Contoh soal 1 dan pembahasannya
Soal :
Carilah jumlah dari deret geometri 2 + 6 + 18 + … + 4374
Jawaban :
a = 2 dan r = 3
Un = arn-1
4374 = 2.(3n-1)
3n-1 =4374 / 2
3n-1 = 2187
3n-1 = 37
n-1 = 7
n = 8
maka S8 = a(rn – 1) / (r – 1)
S8 = 2(38 - 1) / (3 - 1)
S8 = 2 (6560)/ 2
Jadi S8 = 6560
Contoh soal 2 dan pembahasannya
Soal :
Carilah jumlah tujuh suku pertama pada deret geometri 4 + 12 + 36 + 108 +…
Jawaban :
Diketahui a = 4 dan r = 3
S7 = 4(rn - 1) / (r - 1)
S7 = 4(37 - 1) / (3 - 1)
S7 = 4372
Jadi jumlah 7 suku pertama dalam deret tersebut adalah 4372.
Contoh soal 3 dan pembahasannya
Soal :
Tentukan jumlah deret geometri berikut. ini, 4 + 2 + 1 + 1/2 + 1/4 …………..
Jawaban :
Diketahui a = 4 dan r = 1/2
Sn = a / (1 - r)
Sn = 4 / (1 - 1/2)
Sn = 4 / (1/2)
Sn = 4 . 2
Sn = 8
Jadi jumlah deret geometri tersebut adalah 8
Contoh soal 4 dan pembahasannya
Soal :
Suatu jenis bakteri, setiap detik akan membelah diri menjadi dua. Jika pada saat permulaan ada 5 bakteri, berapa waktu yang diperlukan bakteri supaya menjadi 320 bakteri ?`
Jawaban :
Soal tersebut merupakan deret geometri dengan a = 5, r = 2, dan Un = 320
Un = arn-1
320 =5. (2n-1)
(2n-1) = 320/5
(2n-1) = 64
(2n-1) = 2 6
n = 7
Maka waktu yang dibutuhkan bakteri untuk berkembang menjadi 320 adalah 7 menit.
Contoh soal 5 dan pembahasannya
Soal :
Pada sebuah deret geometri diketahui bahwa suku pertamanya adalah 3 dan suku ke-9 adalah 768. tentukan suku ke 7 deret tersebut.
Jawaban :
a = 3 dan U9 = 768
U9 = arn-1
768 = 3.r9-1
768 = 3.r8
r8 =768/3
r8 = 256
r = 2
maka U7 = 3.26. U7 = 194.
6. Pada sebuah deret geometri diketahui bahwa suku pertamanya adalah 3 dan suku ke-9 adalah 768. Suku ke-7 deret tersebut adalah …
Pembahasan :
Diketahui: a = 3
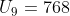
Ditanya: 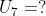
Jawab:
Sebelum kita mencari nilai dari 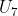 , kita akan mencari nilai r terlebih dahulu.
, kita akan mencari nilai r terlebih dahulu.
Ingat kembali bahwa 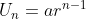 sehingga
sehingga 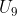 dapat ditulis menjadi
dapat ditulis menjadi
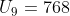
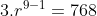
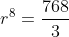
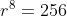
![r=\sqrt[8]{256}](https://latex.codecogs.com/gif.latex?r=\sqrt[8]{256})
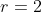
𝑆ehingga,
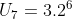
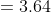
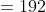
Jadi, suku ke-7 deret tersebut adalah 192.
7. Jumlah 6 suku pertama deret geometri 2 + 6 + 18 + … adalah …
Pembahasan:
Diketahui: a = 2
r = 3
ditanyakan 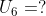
Jawab:
}{(r-1)})
}{(3-1)})
}{2})
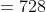
Jadi, jumlah 6 suku pertama deret geometri tersebut adalah 728.
DAFTAR PUSTAKA
https://blog.ruangguru.com/barisan-dan-deret-geometri-rumus-un-sn-dan-deret-geometri-tak-hingga
https://rumus.co.id/geometri/
https://haloedukasi.com/contoh-soal-deret-geometri
https://www.zenius.net/blog/23355/contoh-soal-barisan-dan-deret-geometri

![]() dan
dan ![]() nya, sekarang kita pelajari rumus suku ke – n (
nya, sekarang kita pelajari rumus suku ke – n (![]() ) dan juga rumus jumlah n suku yang pertama (
) dan juga rumus jumlah n suku yang pertama (![]() )
)

![]() nya dan berapa
nya dan berapa![]() adalah jumlah suku ke n pada barisan dan deret. Nah bagaimana cara kita mencari tau
adalah jumlah suku ke n pada barisan dan deret. Nah bagaimana cara kita mencari tau ![]() pada barisan dan deret geometri? Di bawah ini adalah rumusnya.
pada barisan dan deret geometri? Di bawah ini adalah rumusnya. dst. Nah itu adalah cara kita mengetahui berapa S1, S2, S3, dan seterusnya.
dst. Nah itu adalah cara kita mengetahui berapa S1, S2, S3, dan seterusnya.![]() .
.
, kita akan mencari nilai a dan r terlebih dahulu.
maka
Tidak ada komentar:
Posting Komentar