Minggu, 15 November 2020

PERTUMBUHAN, BUNGA TUNGGAL, BUNGA MAJEMUK, BUNGA ANUITAS, PELURUH DAN BEBERAPA CONTOH SOAL

 nama : tabitha fransisca r.n

kelas  : xi ips 3

absen 35

senin, 16 november 2020


Pertumbuhan

Pertumbuhan merupakan kenaikan jumlah pada tiap periode waktu berdasarkan suatu rasio pertumbuhan. Jika jumlah awal adalah 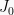J_0 dan rasio adalah r per tahun, maka pada akhir tahun ke-n, jumlah akhirnya menjadi J_n:


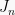CONTOH SOAL PERTUMBUHAN

1. jumlah penduduk 10.000 jiwa dengan pertumbuhan penduduk 5% per tahun, maka pada akhir tahun ke-4, jumlahnya?

jawab :



2. Banyak penduduk kota A setiap tahun meningkat 2% secara eksponensial dari tahun sebelumnya. Tahun 2013 penduduk di kota A sebanyak 150.000 orang. Hitung banyak penduduk pada tahun 2014 dan 2023!

Jawab:

Capture.png

Banyak penduduk pada tahun 2014 (artinya 1 tahun setelah 2013, maka n = 1):

Capture-1.png

Banyak penduduk pada tahun 2023 (n=2023-2013=10):

Bunga

Bunga (suku bunga) atau bank interest adalah pertambahan jumlah modal yang diberikan oleh bank untuk para nasabahnya dengan dihitung dari presentase modal uang nasabah dan lamanya menabung. Bunga juga bisa diberikan oleh pemberi pinjaman kepada pinjaman. Bunga ada dua jenis yaitu bunga tunggal dan bunga majemuk. Berikut ini perbedaannya :

Bunga tunggal 

adalah bunga yang diberikan berdasarkan perhitungan modal awal, sehingga bunga hanya memiliki satu variasi saja (tetap) dari awal periode sampai akhir periode. Contohnya saat menabung di bank, kita akan mendapatkan bunga yang tetap tiap-tiap periode.

Modal adalah jumlah dari yang dibungakan, modal awal merupakan modal yang dikeluarkan pada awal waktu usaha dan sebelum dibungakan. Modal akhir adalah hasil dari modal yang dibungakan.Sedangkan suku bunga dinyatakan dalam persentase tiap satuan waktu.

Jika modal awal sebesar M_0 mendapat bunga tunggal sebesar b (dalam persentase) per bulan, maka setelah n bulan besar modalnya M_n menjadi:

M_n = M_0(1+n \cdot b)

Contoh soal bunga tunggal:

Diketahui modal pinjaman Rp1.000.000 dengan bunga sebesar 2 \% per bulan, maka setelah 5 bulan modalnya adalah ….

M_n = 1.000.000 (1 + 5 \times \frac{2}{100}) = Rp1.100.000

Jika modal awal sebesar M_0, dan diketahui jumlah bunga tunggalnya B, maka besar persentase bunga tunggalnya b adalah

b = \frac{B}{M_0} \times 100 \%

Contoh lain: Diketahui bunga tunggal sebesar Rp50.000 untuk modal pinjaman Rp1.000.000, maka presentasenya adalah

b = \frac{50000}{1000000}\times 100 \% = 5 \%

Bunga majemuk 

adalah bunga yang diberikan berdasarkan modal awal dan akumulasi bunga pada periode sebelumnya.Bunga majemuk memiliki banyak variasi dan selalu berubah (tidak tetap) pada tiap-tiap periode. Contohnya saat menjual sebuah kendaraan, harga kendaraan yang dijualakan berubah setiap periode dan perubahannya bervariasi.


Jika modal awal sebesar M_0 mendapat bunga majemuk sebesar b (dalam persentase) perbulan, maka setelah n bulan besar modalnya M_n menjadi:

M_n = M_0(1+b)^n

CONTOH SOAL BUNGA MAJEMUK

1. diketahui modal pinjaman Rp1.000.000 dengan bunga majemuk sebesar 2 \% per bulan, maka setelah 5 bulan modalnya adalah




Anuitas 

adalah rangkaian pembayaran atau penerimaan yang sama jumlahnya dan harus dibayarkan atau yang harus diterima pada tiap akhir periode atas sebuah pinjaman atau kredit. Jika suatu pinjaman akan dikembalikan secara anuitas, maka ada tiga komponen yang menjadi dasar perhitungan yaitu:

  • Besar pinjaman
  • Besar bunga
  • Jangka waktu dan jumlah periode pembayaran
Anuitas yang diberikan secara tetap pada setiap akhir periode mempunyai dua fungsi yaitu membayar bunga atas hutang dan mengangsur hutang itu sendiri. Sehingga konsepnya :



Jika utang sebesar M_o mendapat bunga sebesar b per bulan dan anuitas sebesar A, maka dapat ditentukan :

  • Besar bunga pada akhir periode ke-n

  • Besar angsuran pada akhir periode ke-n

A_n = (1+b)^{n-1}(A - bM)

  • Sisa hutang pada akhir periode ke-n

M_n = (1+b)^n (M - \frac{A}{b}) + \frac{A}{b}

CONTOH SOAL ANUITAS

1. Sebuah pinjaman sebesar Rp850.000.000,00 yang harus dilunasi dengan 6 anuitas jika dasar bunga 4% per bulan dan pembayaran pertama dilakukan setelah sebulan. Sisa hutang pada akhir bulan kelima adalah?

Pembahasan

A = \frac{b(M_0)(1+b)^n}{(1+b)^n-1}

A = \frac{(0,04)(850.000.000)(1+0,04)^6}{(1+0,04)^6-1}

A = \frac{(0,04)(850.000.000)(1,04)^6}{(1,04)^6-1}

A = \frac{43.020.846,63}{0,2265319}

A = 162.147.628,43

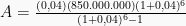
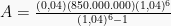
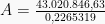
Sisa hutang pada akhir periode ke-5 adalah

M_n = (1+b)^n(M - \frac{A}{b} + \frac{A}{b})

M_n = (1 + 0,04)^5(850.000.000 - \frac{162.147.628,43}{0,04}) + \frac{162.147.628,43}{0,04}

M_n = (1,04)^5(850.000.000 - \frac{162.147.628,43}{0,04}) + \frac{162.147.628,43}{0,04}

M_n = 155.911.109,00


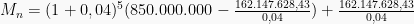
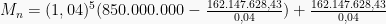
Peluruhan

Peluruhan merupakan penurunan atau pengurangan nilai suatu besaran terhadap nilai besaran sebelumnya yang mengikuti pola aritmatika (linier) atau geometri (eksponensial). Contoh dari peluruhan yaitu peluruhan zat radioaktif dan penurunan harga jual mobil.

Rumus peluruhan linear:

P_n = P_0 (1 - n_b)

Rumus peluruhan eksponensial:

P_n = P_0 (1 - b)^n

Dimana:
P_n = nilai besaran setelah n periode
P_0 = nilai besaran di awal periode
b = tingkat peluruhan
n = banyaknya periode peluruhan

CONTOH SOAL PELURUHAN

1. Suatu bahan radioaktif yang semula berukuran 125 gram mengalami reaksi kimia sehingga menyusut 12% dari ukuran sebelumnya setiap 12 jam secara eksponensial. Tentukan ukuran bahan radioaktif tersebut setelah 3 hari!

Jawab:

Capture-4.png

Peluruhan terjadi setiap 12 jam, sehari peluruhan terjadi 2 kali, 3 hari = 72 jam terjadi 6 kali peluruhan.

Capture-5.png

Capture-6.png

DAFTAR PUSTAKA

https://www.studiobelajar.com/bunga-tunggal-majemuk-anuitas/

https://www.edura.id/blog/matematika/pengertian-bunga/

https://blog.ruangguru.com/pertumbuhan-dan-peluruhan-matematika


di

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

pembelajaran online

 Nama : Tabitha Fransisca R N Kelas  : XI IPS 3 Absen 35       pendapat saya tentang pembelajaran secara online ini ada positif dan negatif....